معادله خمش تیر — از صفر تا صد

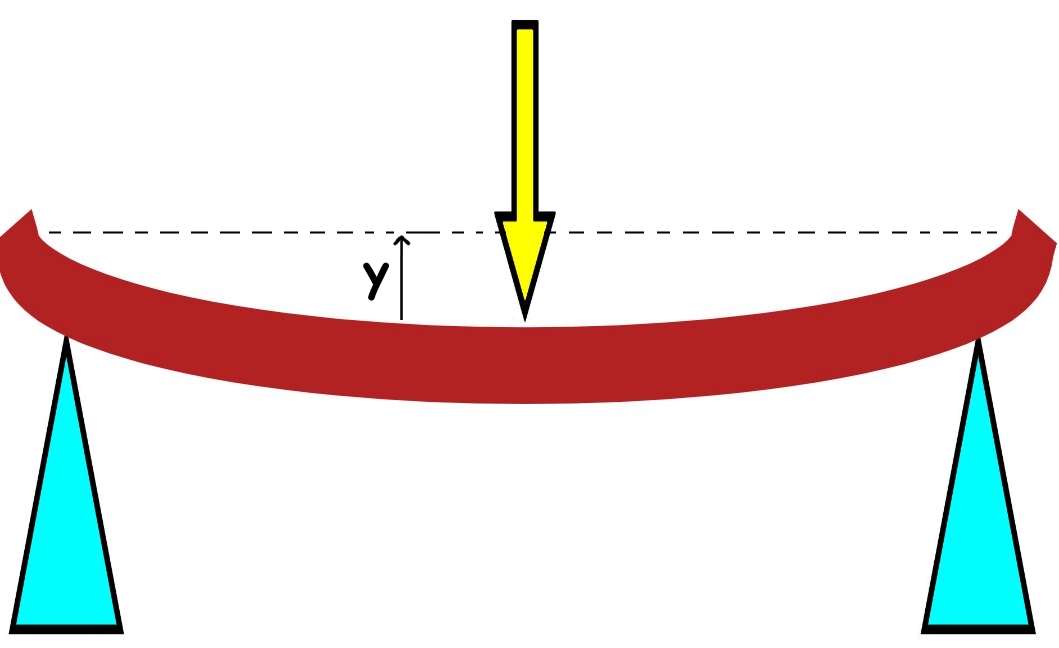
تیر بخشی از یک سازه‌ است که هدف اصلی آن نگه داشتن بار وارد شده به سازه است. در مواردی که خمش تیر اندک باشد می‌توان شکل آن را با استفاده از معادله دیفرانسیلی خطی از مرتبه ۴ مدل‌سازی کرد. از این رو در این مطلب قصد داریم تا تغییر شکل تیر را با استفاده از معادله خمش تیر محاسبه کنیم. البته پیشنهاد می‌شود ابتدا به ساکن مطلب مفاهیم تنش و کرنش را مطالعه فرمایید.

بدست آوردن معادله خمش تیر

در ابتدا فرض کنید که به تیری باری وارد می‌شود. حال دو مقطع از تیر را در نظر بگیرید که در فاصله $$ d x $$ از یکدیگر قرار گرفته‌اند. با وارد شدن نیرو به تیر، دو مقطعی که فاصله آن‌ها $$dx $$ است نسبت به هم به اندازه $$d\theta$$ منحرف می‌شوند.

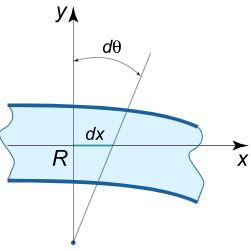
تغییر شکلِ ε در هر نقطه وابسته به مختصات $$y$$ است. این مختصات نسبت به محور میانی تیر اندازه‌گیری می‌شود. توجه داشته باشید که طول خط وسط یا همان محور میانی تیر تغییر شکلی نمی‌دهد. تغییر شکل ε در نتیجه انحراف به اندازه $$y$$ برابر است با:

$$ \varepsilon = \frac { y } { R } $$

در رابطه فوق $$R$$ نشان دهنده شعاع خمش تیر است. اندازه تنش نرمال $$σ$$ در سطح مقطع را می‌توان مطابق با قانون هوک و به صورت زیر بدست آورد.

$$ \large \sigma = \varepsilon E = \frac { E } { R } y $$

$$E$$ نشان دهنده مدول الاستیسیته تیر است. با این فرضیات، گشتاور خمشی وارد شده به تیر نیز برابر است با:

$$ \large { M \left ( x \right ) = { M _ z } } = { \int\limits_A { \sigma y d A } } = {\frac { E }{ R } \int \limits _ A { { y ^ 2 } d A } } = { \frac { E } { R } I } $$

توجه داشته باشید که این گشتاور خمشی در راستای محور $$z$$ قرار می‌گیرد. $$I$$ نشان دهنده لختی دورانی نسبت به محور خنثی $$z$$ است. در شکل زیر مختصات‌های به کار گرفته شده، نشان داده شده است.

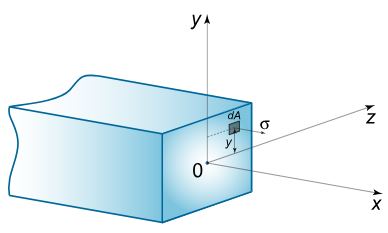
رابطه بدست آمده برای گشتاور را می‌توان به صورت زیر و بر حسب $$R$$ نوشت.

$$ \large R = \frac { { E I } } { { M \left ( x \right ) } } $$

از طرفی از مفاهیم تابع پارامتری می‌دانید که شعاع خمیدگی یک منحنی را می‌توان به صورت زیر تعیین کرد.

$$ \large R = \frac { { { { \left[ {1 + { { \left( { y { \prime } } \right ) }^ 2 } } \right] } ^
{ \large \frac { 3 } { 2 } \normalsize } } } }{ { y ^ { \prime \prime } } } $$

فرض بر این است که میزان انحراف تیر اندک است؛ بنابراین می‌توان از مشتق $$y$$ صرف نظر کرد. از این رو معادله دیفرانسیل یک خط الاستیک به صورت زیر در خواهد آمد.

$$ \large { y ^ { \prime \prime } = \frac { { M \left ( x \right ) } } { { E I } } \;\; \Rightarrow \;\;}\kern-0.3pt { \frac { { { d ^ 2 } y } } { {d { x ^2 } } } = \frac { { M \left ( x \right ) } } { { E I } } } $$

لذا به منظور بدست آوردن شکل یک تیر خمیده شده، کافی است معادله فوق حل شود. بنابراین باید در ابتدا تابعیت گشتاور $$ M ( x ) $$ را نسبت به $$x$$ بدست آورده و پس از حل معادله دیفرانسیل، شکلِ تابع $$y(x)$$ معلوم خواهد شد. اما شاید این سئوال مطرح شود که وابستگی گشتاور نسبت به $$x$$ به چه صورت تعیین می‌شود؟ بدین منظور مطابق با شکل زیر فرض کنید بار $$q(x)$$ به تیری مطابق با شکل زیر وارد می‌شود.

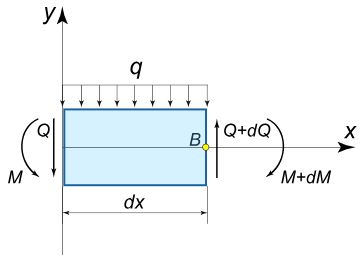
توجه داشته باشید که بار $$q(x)$$ بر حسب نیرو بر واحد طول است. در این صورت معادله تعادل نیرویی روی محور $$y$$، به صورت زیر نوشته می‌شود.

$$ \large { – Q – q d x } + { Q + d Q } = { 0 } $$

هم‌چنین تعادل گشتاور حول محور $$z$$ نیز برابر است با:

$$ \large { – M + M + d M } - { Q d x – q \frac { { { { \left ( { d x } \right ) } ^ 2 } } } { 2 } } = { 0 } $$

با توجه به دو معادله نوشته شده در بالا، وابستگی گشتاور نسبت به $$x$$ برابر است با:

$$\large {\left\{ \begin{array} { l } \frac { { d Q } } { { d x } } = q \\ \frac { { d M } }{ { d x } } = Q \end{array} \right.\;\;}\kern-0.3pt { \Rightarrow \; \; \frac { { { d ^ 2 } M } } { { d { x ^ 2 } } } = q } $$

بنابراین معادله خمش تیر در این حالت از بارگذاری، مطابق با عبارت زیر بدست خواهد آمد.

$$\large \begin {align*} M \left ( x \right ) & = E I \frac { { { d ^ 2 } y } } { { d {
x ^ 2 } } } \Rightarrow {\frac { { { d ^ 2 } M } } { { d { x ^ 2 } } } } \\~\\ & = { \frac { { { d ^2 } } } { { d { x ^ 2 } } } \left ( { E I \frac { { { d ^ 2 } y } } { { d { x ^ 2 } } } } \right) } = { q } \end {align*} $$

عبارت فوق، تحت عنوان معادله دیفرانسیل اویلر-برنولی شناخته می‌شود. اگر مقادیر $$E$$ و $$I$$ در راستای محور $$x$$ ثابت باشند، معادله دیفرانسیلی از مرتبه ۴ به صورت زیر بدست خواهد آمد.

$$ \large E I \frac { { { d ^ 4 } y } } { { d { x ^ 4 } } } = q $$

توجه داشته باشید که برای حل معادله فوق به چهار شرط مرزی نیاز‌مند هستیم. این ۴ شرط مرزی را می‌توان از روی وضعیت تیر بدست آورد. برای نمونه تیر در نقطه‌ای که به تکیه‌گاهش چسبیده، تغییر شکلی نداشته و $$y$$ آن تغییر نمی‌کند؛ بنابراین یکی از شرایط مرزی به صورت $$y(x)=0$$ است. به همین صورت اگر تیر در تکیه‌گاه لولا شده باشد، مشتق $$y$$ نیز در نقطه مذکور برابر با صفر خواهد بود ($$ \frac { d y } { d x } \ ( x = L ) = 0 $$). معادله فوق را می‌توان در حالت بارگذاری گسترده استفاده کرد. در ادامه مثال‌هایی ارائه شده که در آن‌ها نحوه نوشتن شرایط مرزی نیز ارائه شده است.

مثال ۱

تیری را مطابق با شکل زیر در نظر بگیرید که از دو سمت به دیواره‌ای جوش داده شده است. هم‌چنین بارگذاری $$q$$ را در نظر بگیرید که روی آن اعمال شده است. در این صورت معادله تیر پس از اعمال این بارگذاری و بیشترین ارتفاع اِلِمان‌ تیر را بدست آورید. طول اولیه و مدول الاستیسیته را به ترتیب برابر با $$L$$ و $$E$$ در نظر بگیرید.

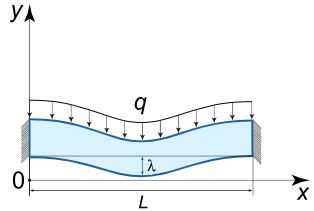
در ابتدا معادله بدست آمده در بالا به صورت زیر نوشته می‌شود.

$$ \large E I \frac { { { d ^ 4 } y } } { { d { x ^ 4 } } } = – q $$

علامت منفی در رابطه فوق نشان می‌دهد که جهت نیروی وارد شده به تیر، عکس جهت $$y$$ است. با توجه به این که دو سمت تیر ثابت شده، لذا می‌توان شرایط مرزی را به صورت زیر بیان کرد:

$$ \large \begin {gather*} {y\left( {x = 0} \right) = 0 \;\;} , \ \kern-0.3pt
{y\left ( {x = L} \right ) = 0 } \\ \kern-0.3pt { \frac { {d y } } { { d x } } \left( { x = 0} \right ) = 0 } \kern-0.3pt \ \ , \ { \frac { { d y } } { { d x } } \left ( { x = L } \right ) = 0 } \end {gather*} $$

حال از معادله خمش تیر، $$4$$ بار انتگرال گرفته و نهایتا شکل کلی معادله خمش برابر می‌شود با:

$$ \large \begin {gather*} { \frac { { { d ^ 3 }y } } { { d { x ^ 3 } } } = – \frac{{qx}}{{ E I } } + { C _ 1 } \;\;} \\~\\ \Rightarrow
{ { \frac { { { d^ 2 }y } } { { d { x ^ 2 } } } = – \frac{{q{x^2}}}{{2EI}} }+{ {C_1}x + { C_ 2 } \;\;}} \\~\\ \Rightarrow
{ {\frac { { d y } } { { d x } } = – \frac { { q {x ^ 3} } }{ { 6 E I } } + \frac { { {C _ 1 }{ x ^ 2} } } { 2 } } + { {C_2}x + {C_3},\;\;} } \\~\\ \Rightarrow
{{y\left( x \right) }={ – \frac{ { q{ x ^ 4 } } } { { 2 4E I } } + \frac { { { C_ 1 } { x ^ 3 }}
} { 6 } }+{ \frac {{ { C _ 2 } { x ^ 2 } } } { 2 } } } + { { { C _ 3 } x } } + { { { C _ 4 } } } \end {gather*} $$

بدیهی است که به منظور بدست آوردن ضرایب، باید از شرایط مرزی استفاده کرد. بنابراین با اعمال $$ y \left ( { x = 0 } \right) = 0 $$ و $$ { \frac {{ d y} } { {d x } } \normalsize}\left( { x = 0 } \right ) = 0 $$، ضرایب $$C_3$$ و $$C_4$$ برابر با صفر بدست می‌آیند ($$ C _ 4 , C_ 3 = 0 $$). از طرفی با اعمال شرایط مرزی در $$x=L$$ داریم:

$$ {\left \{ \begin{array}{l}
{{\Large { – \frac { { q { L ^ 4 } } } { { 2 4 E I } } + \frac { { {C _ 1} { L ^ 3 } } } { 6 } }+{ \frac { { {C _ 2 } { L ^ 2 } } } { 2 } = 0 } } } \\ { \Large { { – \frac { {q { L ^ 3} } } { { 6 E I} } + \frac { { { C_ 1 } { L ^ 2} } } { 2 } } } } + { { C _ 2 } L = 0}
\end {array} \right.} $$

با حل دو دستگاه معادلات بالا، مقادیر $$C_2$$ و $$C_1$$ برابرند با:

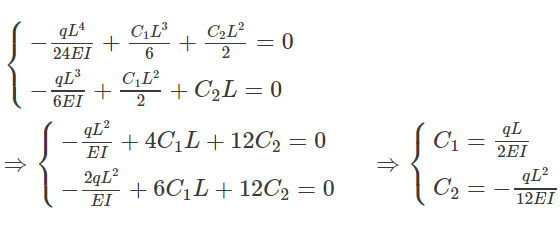
بنابراین نهایتا شکل تیر مطابق با رابطه زیر بدست خواهد آمد.

$$ \large \begin {align*} { y \left( x \right) } & = { – \frac { {q { x ^ 4 } } } { { 2 4 E I } } + \frac { { q L { x ^ 3 } } } { { 1 2 EI } } } - { \frac { { q { L ^2 } { x ^ 2 } } } { { 24 E I } } } \\ & = { – \frac { {q { x ^ 2 } } } { { 2 4 E I } } \left ( { { x ^ 2 } – 2Lx + { L ^2 } } \right) } \\ & = { – \frac { { q { x ^ 2 } } } { { 24 E I } } { \left ( { x – L } \right ) ^ 2 } } \end {align*} $$

به منظور بدست آوردن بیشترین تغییر طول، از مفهوم ماکزیمم، مینیمم نسبی استفاده می‌کنیم. ثابت‌ها را از تابع $$y$$ جدا کرده و مابقی را $$f$$ می‌نامیم. بدین منظور در اولین قدم باید مشتق $$f$$ را به صورت زیر برابر با صفر قرار دهیم.

$$ \large \begin {align*} f ^ { \prime } \left( x \right) & = { \left[ { { x ^ 2 } { { \left( {x – L} \right ) } ^ 2 } } \right] ^ \prime } \\ & = { 2 x { \left ( { x – L } \right ) ^ 2 } + 2 { x ^ 2 } \left ( { x – L } \right ) } \\ & = { 2 x \left( {x – L} \right ) \left ( { x – L + x } \right ) } = { 2 x \left ( { x – L } \right ) \left ( { 2 x – L } \right) } \\ & = { 0 } \end {align*} $$

همان‌طور که از معادله فوق نیز دیده می‌شود، مشتق تابع در نقطه $$x=\frac{L}{2}$$ برابر با صفر است. در این نقطه مقدار تابع $$f$$ برابر است با:

$$\large { { f \left ( { \frac { L } {2 } } \right) } = { { \left( { \frac { L} { 2 } } \right ) ^ 2 } { \left ( { – \frac { L} { 2} } \right ) ^ 2 } } = { \frac { { { L ^ 4 } } }{ { 16 } } }} $$

در نتیجه نهایتا بیشترین تغییر طولِ تیر در $$ \large x = \frac { L } { 2 } $$ رخ داده و مقدار آن نیز برابر است با:

$$ \large x = \frac { L } { 2 } $$

مثال ۲

شفتی استوانه‌ای و نازک به طول $$L$$ را در نظر بگیرید که با سرعت زاویه‌ای $$ \omega $$ دوران می‌کند. مدول الاستیسیته، جرم و شعاع این شفت را به‌ ترتیب برابر با $$E$$، $$M$$ و $$a$$ در نظر بگیرید. با این فرضیات این شفت تا چه سرعت زاویه‌‌ای مجاز به دوران است؟

زمانی که شفت حرکتی دایره‌ای انجام می‌دهد، نیرویی گریز از مرکز در آن بوجود می‌آید. اندازه این نیرو در هر دیفرانسیل از شفت، وابسته به فاصله آن از محور دوران است. این فاصله را در معادلات با $$y$$ نمایش می‌دهیم. با افزایش فاصله از محور دوران، اندازه نیروی گریز از مرکز نیز افزایش خواهد یافت. این نیرو در سرعت‌های زاویه‌ای خاصی تشدید شده و منجر به از بین رفتن سیستم می‌شود.

همان‌طور که در بالا نیز بیان شد، اگر نیرویی مقطعی به یک تیر وارد شود، معادله خمش آن مطابق با معادله دیفرانسیل زیر توصیف می‌شود.

$$\large E I \frac { { { d ^ 4 } y } } { { d { x ^ 4} } } = f $$

در رابطه فوق، $$f$$ نشان دهنده چگالی نیروی گریز از مرکز است. از طرفی نیروی گریز از مرکز وارد شده به دیفرانسیل $$ d x $$ برابر است با:

$$ \large d F = { \omega ^ 2 } y \frac { M } { L } d x $$

در رابطه فوق، $$ { \frac { M } { L } \normalsize } d x $$ نشان دهنده جرمِ المان $$dx$$ بوده، $$y$$ نیز میزان انحراف المان $$dx$$ از محور دوران را نشان می‌دهد. با این فرضیات معادله دیفرانسیل فوق به صورت زیر قابل بازنویسی است.

$$ \large { E I \frac { { { d ^ 4 } y } } { { d { x ^4 } } } = \frac { { { \omega ^ 2 } M } } { L } y \;\;\;} \kern-0.3pt { \Rightarrow \;\;\;\frac { { { d ^ 4 } y } } { { d{ x ^ 4 } } } – { \alpha ^ 4 } y = 0 } $$

ارتباط بین $$\alpha$$ و $$\omega$$ در رابطه بالا به صورت زیر است.

$$ \large { \alpha ^ 4 } = { \large \frac { { { \omega ^ 2 } M } } { { E I L} } \normalsize } $$

معادله مشخصه مرتبط با معادله دیفرانسیل فوق، برابر است با:

$$ \large { \alpha ^ 4 } = { \large \frac { { { \omega ^ 2 } M } } { { E I L } } \normalsize } $$

در نتیجه ریشه‌ها برابرند با:

$$ \large { { s _ 1 } = \alpha ,\;\;{ s _ 2 } = – \alpha ,\;\;} \kern-0.3pt
{ { s _ 3 } = \alpha i , \;\; { s _ 4 } = – \alpha i } $$

بنابراین پاسخ عمومی این معادله برابر با رابطه زیر بدست خواهد آمد.

$$ \large { y \left ( x \right ) } = { { C _ 1 } { e ^ { \alpha x } } + { C _ 2 } { e ^ { – \alpha x } } } + { { C _ 3 } \cos \alpha x + { C _ 4 } \sin \alpha x } $$

ضرایب $$ C $$ با توجه به معادله دیفرانسیل بدست می‌آیند. این شفت از دو سمت در دو یاتاقان قرار گرفته است. بنابراین در این نقاط جابجایی نداشته و انحنای آن نیز صفر است. لذا:

• جابجایی شفت در دو نقطه $$ x = 0 $$ و $$ x = L $$ برابر با $$y = 0 $$ است.
• انحنای شفت در دو نقطه $$ x = 0 $$ و $$ x = L $$ برابر با $$ \frac { d ^ 2 y } { d x ^ 2 } = 0 $$ است.

به بیانی ریاضیاتی می‌توان گفت:

$$\large \begin {gather*} { y \left( { x = 0 } \right) = 0 \;\;}\kern-0.3pt{y\left( {x = L} \right) = 0 } \\~\\ \kern-0.3pt { \frac { { { d ^ 2 } y } } { { d { x ^ 2 } } }\left ( { x = 0 } \right ) = 0 \;\;} \kern-0.3pt { \frac { { { d ^ 2 } y } } { { d { x ^ 2 } } } \left ( { x = L } \right ) = 0 } \end {gather*} $$

از طرفی مشتق دوم $$ y $$ نسبت به $$ x $$ نیز مطابق با رابطه زیر بدست خواهد آمد.

$$\large \begin {gather*} { \frac { { d y } } { { d x } } }={ {C_1}\alpha { e ^ { \alpha x } } } - { { C _ 2 } \alpha { e ^ { – \alpha x}} } – { { C _ 3 } \alpha \sin \alpha x }
+ { { C _ 4 } \alpha \cos\alpha x } \\‍‍‍‍‍‍‍\\ { \frac { { { d^ 2 }y } } { { d { x ^ 2 } } } } = { { C _ 1 } { \alpha ^ 2 } { e ^ { \alpha x } } } + { { C _ 2 } { \alpha ^ 2 } { e ^ { – \alpha x } } }
– { { C _3 } { \alpha ^ 2 } \cos \alpha x } – { { C _ 4 } { \alpha ^ 2 } \sin \alpha x } \end {gather*} $$

با قرار دادن $$ y $$ و $$ \frac { { { d^ 2 } y} } {{ d { x ^ 2} } } \normalsize $$ در شرایط مرزی،‌ رابطه مربوط به ضرایب ثابت، برابرند با:

$$\large \left\{ \begin{array} { l }
{ C _ 1 } + { C _ 2 } + { C _ 3 } = 0 \\
{ C _ 1 } + { C _ 2 } – { C _ 3 } = 0 \\
{ { C _ 1 } { e ^ { \alpha L } } + { C _ 2 } { e ^ { – \alpha L } } } + { { C _ 3 } \cos \alpha L } + { { C_ 4 } \sin \alpha L } = { 0 } \\
{ { C _ 1 } { e ^ { \alpha L } } + { C _2 } { e ^ { – \alpha L } } } - { { C_ 3 } \cos \alpha L } - { { C _ 4 } \sin \alpha L } = { 0 }
\end {array} \right. $$

بنابراین ضرایب مطابق با روابط زیر بدست خواهند آمد:

$$ \large \left \{ \begin {array} { l }
{ C _ 1 } = 0 \\
{ C _ 2 } = 0 \\
{ C_ 3 } = 0 \\
{ C _ 4 } \sin \alpha L = 0
\end {array} \right.$$

در رابطه آخر اگر $$ { C _ 4 } = 0 $$ در نظر گرفته شود، در این صورت پاسخ بدیهی $$ y = 0 $$ بدست خواهد آمد. این حالت، معادل با آن است که شفت هیچ تغییر شکلی نداده باشد. بنابراین به منظور دست‌یابی به پاسخی با معنی باید ضریب سینوس را برابر با صفر قرار داده و $$\alpha$$ متناسب با آن را بدست آورد. با انجام این کار داریم:

$$ \large { \sin \alpha L = 0 \; } \Rightarrow { \alpha L = \pi n,\; \; \; \; } \kern-0.3pt {n = 1 , 2 ,3 , \ldots } $$

توجه داشته باشید که مقادیر $$n$$ بیشتر از صفر در نظر گرفته می‌شوند. در حقیقت با فرض $$n=0$$ به پاسخ بدیهی $$y=0$$ خواهیم رسید. نهایتا با فرض $$ \alpha L = \pi n $$، شکل شفت به صورتی سینوسی در خواهد آمد. رابطه زیر توصیف کننده تغییر شکل شفت در نتیجه دوران با سرعت زاویه‌ای $$\alpha$$ است.

$$ \large { y \left ( x \right ) = { C _ 4 } \sin \alpha x } = { { C _ 4 } \sin \left ( {\frac { { \pi n } } { L} x } \right ) } $$

با فرض $$n=1$$، کمترین سرعت زاویه‌ای بحرانی مطابق با رابطه زیر بدست خواهد آمد.

$$ \large \begin {align*} \alpha & = \frac{\pi }{L}\left( {\text{at}\;n = 1} \right) \\\\ & \Rightarrow
{\frac{{\omega _\text{c}^2M}}{{EIL}} = {\alpha ^4} = {\left( {\frac{\pi }{L}} \right)^4}\;\;} \\\\ & \Rightarrow
{{\omega _\text{c}^2 = \frac{{{\pi ^4}} }{ {{ L^4} }}\frac { {E I L }} { M } }={ \frac{{{\pi ^4}}}{{{L^3}}}\frac { { EI } } {M }\;\;}} \\\\ & \Rightarrow
{{\omega _\text{c}} = \frac { { { \pi ^ 2 }} }{ L}\sqrt { \left( \frac { { E I } } {{ L M } } \right) } } \end {align*} $$

اگر شفت، به صورت میله‌ای جامد با شعاع $$ a $$ در نظر گرفته شود، در این صورت لختی دورانی آن حول محور دوران برابر است با:

$$ \large I = \frac { { M { a ^ 2 } } } { { 4 L} } $$

با قرار دادن $$I$$ در رابطه مربوط به $$\omega_c$$، نهایتا سرعت زاویه‌ای بحرانی برابر خواهد بود با:

$$ \begin {align*} { { \omega _ \text {c}} } = { \frac { { { \pi ^2} } }{L} \sqrt { \left ( \frac { { EI } } { { L M } } \right ) } } & = { \frac { { { \pi ^ 2 } } } { L } \sqrt {\left( {\frac { E } { { L M } } \cdot \frac { {M { a ^ 2 } } }{{4L}} } \right)} } \\ \\ & = {\frac { { { \pi ^ 2 } a } } { { 2 { L^ 2 } } }\sqrt E } \end {align*} $$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی عمران و مکانیک، آزموش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• مجموعه آموزش های مهندسی عمران
• مجموعه آموزش‌های نرم‌افزارهای مهندسی عمران و معدن
• آموزش مقاومت مصالح