مشتق cotx — به زبان ساده

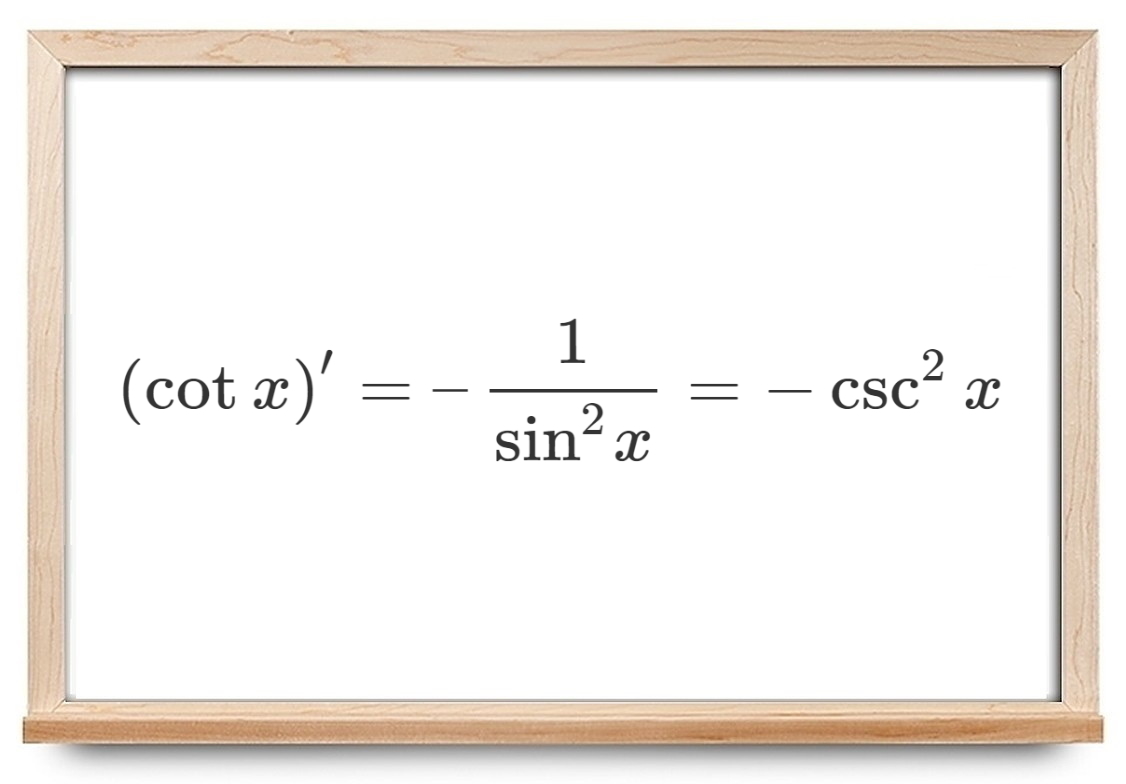
در آموزش‌های قبلی مجله فرادرس، با مشتق توابع مثلثاتی آشنا شدیم. در این آموزش با تمرکز بیشتری درباره مشتق cotx بحث می‌کنیم و مثال‌های متنوعی را حل خواهیم کرد.

فرمول محاسبه مشتق cotx

فرمول محاسبه مشتق cotx به صورت زیر است:

$$ \large \begin {align*} \require {cancel} { \left ( { \cot x } \right ) ^ \prime } = { – \frac { 1 } { { { { \sin } ^ 2 } x } } } = - \csc ^ 2 x \end {align*}. $$

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

اثبات فرمول محاسبه مشتق cotx

اتحادی که سه تابع $$ \sin x $$، $$ \cos x $$ و $$ \cot x $$ را به هم ربط می‌دهد به صورت زیر است:

$$ \large \cot x = \dfrac { \cos x } { \sin x } $$

اکنون از قاعده خارج قسمت برای مشتق‌گیری استفاده می‌کنیم:

$$ \large { \dfrac { d } { d x } \cot x = \dfrac { d } { d x } ( \dfrac { \cos x } { \sin x } ) = \dfrac { { ( \dfrac { d } { d x } \cos x ) } { \sin x } - \cos x ( \dfrac { d } { d x } \sin x ) }{ \sin ^ 2 x } } $$

حال، از دو فرمول $$ \dfrac {d}{dx}\cos x = - \sin x $$ و $$\dfrac {d}{dx}\sin x = \cos x $$ استفاده می‌کنیم و خواهیم داشت:

$$ \large { \dfrac { d } { d x } \cot x = \dfrac { { - \sin x \sin x } - \cos x \cos x } { \sin ^ 2 x } } $$

و با ساده‌سازی، داریم:

$$ \large { = - \dfrac { \sin ^ 2 x + \cos ^ 2 x } { \sin ^ 2 x } = - \dfrac { 1 } { \sin ^ 2 x } = - \csc ^ 2 x } $$

البته، یک راه دیگر محاسبه مشتق cotx استفاده از مشتق تابع تانژانت و قاعده زنجیره‌ای است:

$$ \large \begin {align*} \require {cancel}  { \left ( { \cot x } \right ) ^ \prime } & = \left ( { \frac { 1 } { { \tan x } } }   \right ) ^ \prime   = { – \frac { 1 } {  { { { \tan } ^ 2 } x } }  \cdot { \left ( { \tan x }  \right ) ^ \prime } } \\ & = { – \frac { 1 } { { \frac { { { { \sin } ^ 2 } x } } { { {  { \cos } ^ 2 } x } } } }  \cdot \frac { 1 } { { { {  \cos } ^ 2 } x } }   }  = { – \frac { \cancel { { { \cos } ^ 2 } x } }{  { { { \sin } ^ 2 } x  \cdot \cancel { { {  \cos } ^ 2 } x  } } }   }   = { – \frac { 1 } { { {  { \sin } ^ 2 } x } }. }   \end {align*} $$

فرمول محاسبه مشتق cotu

اما اگر مشتق cotu را به جای مشتق cotx داشته باشیم که u خود یک تابع است، می‌توانیم از قاعده زنجیره‌ای برای مشتق‌گیری استفاده کنیم:

$$ \large \dfrac { d } { d x } \cot ( u ( x ) ) = ( \dfrac { d } { d u } \cot u ) ( \dfrac { d } { d x } u ) $$

و با ساده‌سازی خواهیم داشت:

$$ \large = - \csc ^ 2 u \dfrac { d } { d x } u $$

مثال‌های محاسبه مشتق cotx

در این بخش، مثال‌هایی از محاسبه مشتق cotx و cotu را حل می‌کنیم.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

مثال 1 مشتق cotx

مشتق تابع زیر را محاسبه کنید.

$$ \large f ( x ) = \cot ( x ^ 3 - 2 x + 2 ) $$

حل: تابع $$ u(x) = x^3-2x+2 $$ و در نتیجه، $$ \dfrac{d}{dx} u = \dfrac{d}{dx} (x^3-2x+2) = 3x^2-2 $$ را در نظر می‌گیریم و از قاعده مشتق کتانژانت استفاده می‌کنیم:

$$ \large \begin {align*} \dfrac { d } { d x } f ( x ) & = - \csc ^ 2 u \dfrac { d } { d x } u = - \csc ^ 2 ( x ^ 3 - 2 x + 2 ) \times ( 3 x ^ 2 - 2 ) \\
& = - ( 3 x ^ 2 - 2 ) \csc ^ 2 ( x ^ 3 - 2 x + 2 )
\end {align*} $$

مثال 2 مشتق cotx

مشتق تابع زیر را محاسبه کنید.

$$ \large g(x) = \cot (e^x) $$

حل: با در نظر گرفتن $$ u(x) = e^x $$ و در نتیجه، $$ \dfrac { d } { d x } u = \dfrac { d } { d x } e ^ x = e ^ x $$ و استفاده از قاعده مشتق کتانژانت، خواهیم داشت:

$$ \large \dfrac { d } { d x } g ( x ) = - \csc ^ 2 u \dfrac { d }{ d x } u = - \csc ^ 2 ( e ^ x ) \times e ^ x = - e ^ x \csc ^ 2 ( e ^ x ) $$

مثال 3 مشتق cotx

مشتق تابع زیر را به دست آورید.

$$ \large h ( x ) = \cot ( \dfrac { - 2 } { x ^ 3 + 2 } ) $$

حل: تابع $$ u(x) = \dfrac{-2}{x^3+2} $$ و مشتق آن، $$ \dfrac{d}{dx} u = \dfrac{6x^2}{\left(x^3+2\right)^2} $$، را در نظر بگیرید. از قاعده مشتق کتانژانت استفاده می‌‌کنیم:

$$ \large \begin {align*} \dfrac { d } { d x } h ( x ) & = - \csc ^ 2 u \dfrac { d } { d x } u = - \csc ^ 2 ( \dfrac { - 2 } { x ^ 3 + 2 } ) \times \dfrac { 6 x ^ 2 } { \left ( x ^ 3 + 2 \right ) ^ 2 } \\
& = - \dfrac { 6 x ^ 2 } { \left ( x ^ 3 + 2 \right ) ^ 2 } \csc ^ 2 ( \dfrac { - 2 } { x ^ 3 + 2 } ) = - \dfrac { 6 x ^ 2 } { \left ( x ^ 3 + 2 \right ) ^ 2 } \csc ^ 2 ( \dfrac { 2 } { x ^ 3 + 2 } )
\end {align*} $$

مثال 4 مشتق cotx

مشتق عبارت زیر را محاسبه کنید.

$$ \large y = \tan \frac{x}{2} – \cot \frac{x}{2} $$

حل: در اولین گام، داریم:

$$ \large { y’ \left ( x \right ) } = { { \left ( { \tan \frac { x } { 2 } – \cot \frac { x } { 2 } } \right ) ^ \prime } } = { { \left ( { \tan \frac { x } { 2 } } \right ) ^ \prime } – { \left ( { \cot \frac { x } { 2 } } \right ) ^ \prime } . } $$

روابط زیر را می‌دانیم:

$$ \large { { \left ( { \tan x } \right ) ^ \prime } = \frac { 1 }{ { { { \cos } ^ 2 } x } } , \; \; \; } \kern-0.3pt { { \left ( { \cot x } \right ) ^ \prime } = – \frac { 1 } { { { { \sin } ^ 2 } x } } , } $$

با استفاده از مشتق cotx و قاعده زنجیره‌ای، می‌توانیم بنویسیم:

$$ \large \begin {align*}
y’ \left ( x \right ) & = { \frac { 1 } { { { { \cos } ^ 2 } \frac { x } { 2 } } } \cdot { \left ( { \frac { x } { 2 } } \right ) ^ \prime } } - { \left ( { – \frac { 1 } { { { { \sin } ^ 2 } \frac { x } { 2 } } } } \right ) \cdot { \left ( { \frac { x } { 2 } } \right ) ^ \prime } } \\ & = { \frac { 1 } { { { { \cos } ^ 2 } \frac { x } { 2 } } } \cdot \frac { 1 } { 2 } + \frac { 1 } { { { \sin ^ 2 } \frac { x } { 2 } } } \cdot \frac { 1 } { 2 } } = { \frac { { { \sin ^ 2 } \frac { x } { 2 } + { { \cos } ^ 2 } \frac { x } { 2 }} } { { 2 \, { { \cos } ^ 2 } \frac { x } { 2 } { \sin ^ 2 } \frac { x } { 2 } } } . }
\end {align*} $$

برای ساده کردن عبارت، از اتحادهای مثلثاتی $$ {\sin^2}x + {\cos ^2}x = 1 $$ و $$ \sin x = 2\sin {\large\frac{x}{2}\normalsize} \cos {\large\frac{x}{2}\normalsize} $$ استفاده می‌کنیم و خواهیم داشت:

$$ \large \begin {align*}
{ y’ \left ( x \right ) } = { \frac { 1 } { { 2 { { \cos } ^ 2 } \frac { x } { 2 } { \sin ^ 2 } \frac { x } { 2 } } } } = { \frac { { 2 \cdot 1 } } { { 4 { { \cos } ^ 2 } \frac { x } { 2 }{ \sin ^ 2 } \frac { x } { 2 } } } } = { \frac { 2 } { { { { \left ( { 2 \cos \frac { x } { 2 } \sin \frac { x } { 2 } } \right ) } ^ 2 } } } } = { \frac { 2 } { { { { \sin } ^ 2 } x } } . }
\end {align*} $$

مثال 5 مشتق cotx

مشتق تابع زیر را به دست آورید.

$$ \large y = \frac{{{{\sin }^2}x}}{{1 + \cot x}} + \frac{{{{\cos }^2}x}}{{1 + \tan x}} $$

حل: تابع را برحسب سینوس و کسینوس می‌نویسیم و ساده می‌کنیم:

$$ \large \begin {align*}
y & = \frac { { { { \sin } ^ 2 } x } } { { 1 + \cot x } } + \frac { { { { \cos } ^ 2 } x } } { { 1 + \tan x } } = { \frac { { { { \sin } ^ 2 } x} } { { 1 + \frac { { \cos x } } { { \sin x } } } } + \frac { { { { \cos } ^ 2 } x } } { { 1 + \frac { { \sin x } } { { \cos x } } } } } \\ & = { \frac { { { { \sin } ^ 2 } x } }{ { \frac { { \sin x + \cos x } } { { \sin x } } } } + \frac { { { { \cos } ^ 2 } x } } { { \frac { { \cos x + \sin x } } { { \cos x } } } } } = { \frac { { { { \sin } ^ 3 } x } } { { \sin x + \cos x } } + \frac { { { { \cos } ^ 3 } x } } { { \sin x + \cos x } } } \\ & = { \frac { { { { \sin } ^ 3 } x + { { \cos } ^ 3 } x } } { { \sin x + \cos x } } . }
\end {align*} $$

اکنون برای ساده کردن مجدد کسر، از اتحاد زیر استفاده می‌کنیم:

$$ \large { { a ^ 3 } + { b ^ 3 } } = { \left ( { a + b } \right ) \left ( { { a ^ 2 } – a b + { b ^ 2 } } \right ) } $$

که منجر به عبارت زیر می‌شود:

$$ \large y = {\sin ^2}x – \sin x\cos x + {\cos ^2}x. $$

و در نهایت، جواب مسئله با استفاده از قوانین مشتق cotx و  مشتق زنجیره‌ای و ضرب و با کمک جدول مشتق توابع مثلثاتی پایه به دست می‌آید:

$$ \large \begin {align*}
y ^ \prime & = \left ( { { { \sin } ^ 2 } x } \right ) ^ \prime - { \left ( { \sin x \cos x } \right ) ^ \prime } + { \left ( { { { \cos } ^ 2 } x } \right ) ^ \prime } \\ & = { 2 \sin \cos x } - { \left ( { \sin x } \right ) ^ \prime \cos x } - { \sin x \left ( { \cos x } \right ) ^ \prime } + { 2 \cos x \left ( { – \sin x } \right ) } \\ & = { \cancel { 2 \sin x \cos x } } - { { \cos ^ 2 } x } + { { \sin ^ 2 } x } - { \cancel { 2 \sin x \cos x } } \\ & = { – \left ( { { { \cos } ^ 2 } x – { { \sin } ^ 2 } x } \right ) } = { – \cos 2 x . }
\end {align*} $$

مثال 6 مشتق cotx

مشتق تابع زیر را بیابید.

$$ \large 2 \sqrt { \cot ( x ^ 2 ) } $$

حل: مشتق این تابع به صورت زیر محاسبه می‌شود:

$$ \large \begin {align*} y' & = \left ( 2\sqrt { \cot ( x ^ 2 ) } \right )' = 2 \left ( \sqrt { \cot ( x ^ 2 ) } \right )'
= 2 \frac { 1 } { 2 \sqrt { \cot ( x ^ 2 ) } } \cdot \left (\cot (x^2)\right)' \\
& = \frac { 1 } { \sqrt { \cot ( x ^ 2 ) } } \cdot \left ( - \csc ^ 2 (x^2) \cdot (x^2)'\right)
= \frac { 1 } { \sqrt { \cot ( x ^ 2 ) } } \cdot \left ( -csc ^2 (x^2)\right ) \cdot 2 x \\
& = \frac {-2x\csc ^ 2 (x^ 2) }{\sqrt { \cot ( x ^ 2 ) } }
= \frac {-2x } { \sin ^ 2 ( x ^ 2 ) \cdot \sqrt \frac {\cos (x^2)}{ \sin ( x ^ 2 ) } } = \frac {-2x } { \sin ( x ^ 2 ) \cdot \sin ( x ^ 2 ) \sqrt \frac {\cos (x^2)}{\sin (x^ 2)}} \\
& = \frac {-2x } { \sin ( x ^ 2 ) \cdot \sqrt { \sin ^ 2 ( x ^ 2 ) \frac {\cos (x^2)}{\sin (x^ 2 ) } } } = \frac {-2x } { \sin ( x ^ 2 ) \cdot \sqrt { {\cos (x^2)}{\sin (x^ 2)}}} \\ &= \frac {-2x } { \sin ( x ^ 2 ) \cdot \sqrt {\frac 2 2 {\cos ( x ^ 2 ) } { \sin ( x ^ 2 ) } } } = \frac { - 2 \sqrt 2 x } { \sin ( x ^ 2 ) \cdot \sqrt { 2 { \cos ( x ^ 2 ) } { \sin ( x ^ 2 ) } } } \\
& = \frac { - 2 \sqrt 2 x } { \sin ( x ^ 2 ) \cdot \sqrt { {\sin ( 2x ^ 2 ) } { } } }
\end {align*} $$

مثال 7 مشتق cotx 

مشتق ضمنی $$ 3 \cot ( x + y ) = \cos y ^ 2 $$ را محاسبه کنید.

حل: از تغییر متغیر $$ u = x + y $$ استفاده می‌کنیم. مشتق $$ 3 \cot u $$ برابر خواهد بود با:‌

$$ \large { 3 } { \left ( - { { \csc } ^ { 2 } { u } } \right ) }{ \left ( \frac { { { d } { u } } } { { { \left . { d }{ x } \right . } } } \right ) } $$

مقدار $$ u $$ و $$ \frac { d u } { d { x }} $$ را در رابطه بالا قرار می‌دهیم:

$$ \large - { 3 } { { \csc } ^ { 2 } { \left ( { x } + { y } \right ) } } { \left ( { 1 } + \frac { { { \left . { d } { y } \right . } } }{ { { \left . { d } { x } \right . } } } \right ) } $$

در سمت راست از تغییر متغیر $$ u = y ^ 2 $$ استفاده می‌کنیم. مشتق $$ \cos u $$ برابر است با:

$$ \large { \left ( - \sin { { u } } \right ) } { \left ( \frac { { { d } { u } } } { { { \left . { d } { x } \right . } } } \right ) } $$

با جایگذاری مقدار $$u $$ و محاسبه $$ \frac { d u } { d x } $$، خواهیم داشت:

$$ \large { \left ( - \sin { { y } } ^ { 2 } \right ) } { \left ( { 2 }{ y } \frac { { { \left . { d } { y } \right . } } } { { { \left . { d } { x } \right . } } } \right ) } $$

دو طرف را برابر قرار می‌دهیم:

$$ \large - { 3 } { { \csc } ^ { 2 } { \left ( { x } + { y } \right ) } } { \left ( { 1 } + \frac { { { \left . { d } { y } \right . } } } { { { \left . { d } { x } \right . } } } \right ) } = { \left ( - \sin { { y } } ^ { 2 } \right ) } { \left ( { 2 } { y } \frac { { { \left . { d } { y } \right . } } } { { { \left . { d } { x } \right . } } } \right ) } $$

با بسط جملات، می‌توان نوشت:

$$ \large - { 3 } { { \csc } ^ { 2 } { \left ( { x } + { y } \right ) } } - { 3 } { { \csc } ^ { 2 } { \left ( { x } +{ y } \right ) } } \frac { { { \left . { d } { y } \right . } } } { { { \left . { d }{ x } \right . } } } = - { 2 } { y } \frac { { \sin { { y } } ^ { 2 } { \left ( { \left . { d } { y } \right . } \right ) } } } { { { \left . { d } { x } \right . } } } $$

با اضافه کردن $$ { 2 } { y } \frac { { \sin { { y } } ^ { 2 } { \left ( { \left .{ d } { y } \right . } \right ) } } } { { { \left . { d } { x } \right . } } } $$ به دو طرف رابطه بالا، داریم:

$$ \large - { 3 } { { \csc } ^ { 2 } { \left ( { x } + { y } \right ) } } - { 3 } { { \csc } ^ { 2 } { \left ( { x } +{ y } \right ) } } \frac { { { \left . { d } { y } \right . } } } { { { \left . { d }{ x } \right . } } } + { 2 } { y } \frac { { \sin { { y } } ^ { 2 } { \left ( { \left . { d } { y } \right . } \right ) } } } { { { \left .{ d } { x } \right . } } }= { 0 } $$

اکنون $$ { 3 } { { \csc } ^ { 2 } { \left ( { x } + { y } \right ) } } $$ را به طرفین رابطه اخیر اضافه می‌کنیم و خواهیم داشت:

$$ \large - { 3 } { { \csc } ^ { 2 } { \left ( { x } +{ y } \right ) } } \frac { { { \left . { d } { y } \right . } } } { { { \left . { d } { x } \right . } } } + { 2 } { y } \frac { { \sin { { y } } ^ { 2 } { \left ( { \left . { d } { y } \right . } \right ) } } } { { { \left . { d } { x } \right . } } } = { 3 } { { \csc } ^ { 2 } { \left ( { x } + { y } \right ) } } $$

از $$ dy / dx $$ فاکتور می‌گیریم:

$$ \large { \left [ { 2 } { y } { \sin { { y } } ^ { 2 } - } { 3 }{ { \csc } ^ { 2 } { \left ( { x } + { y } \right ) } } \right ] } \frac { { { \left . { d } { y } \right . } } } { { { \left . { d }{ x } \right . } } } = { 3 } { { \csc } ^ { 2 } { \left ( { x } + { y } \right ) } } $$

و در نهایت، جواب به صورت زیر است:

$$ \large \frac { { { \left . { d } { y } \right . } } } { { { \left .{ d } { x } \right . } } } = \frac { { { 3 } { { \csc } ^ { 2 }{ \left ( { x } + { y } \right ) } } } } { { { 2 } { y } { \sin { { y } } ^ { 2 } } } } - \ { 3 } { { \csc } ^ { 2 } { \left ( { x } + { y } \right ) } } $$