مشتق انتگرال — به زبان ساده

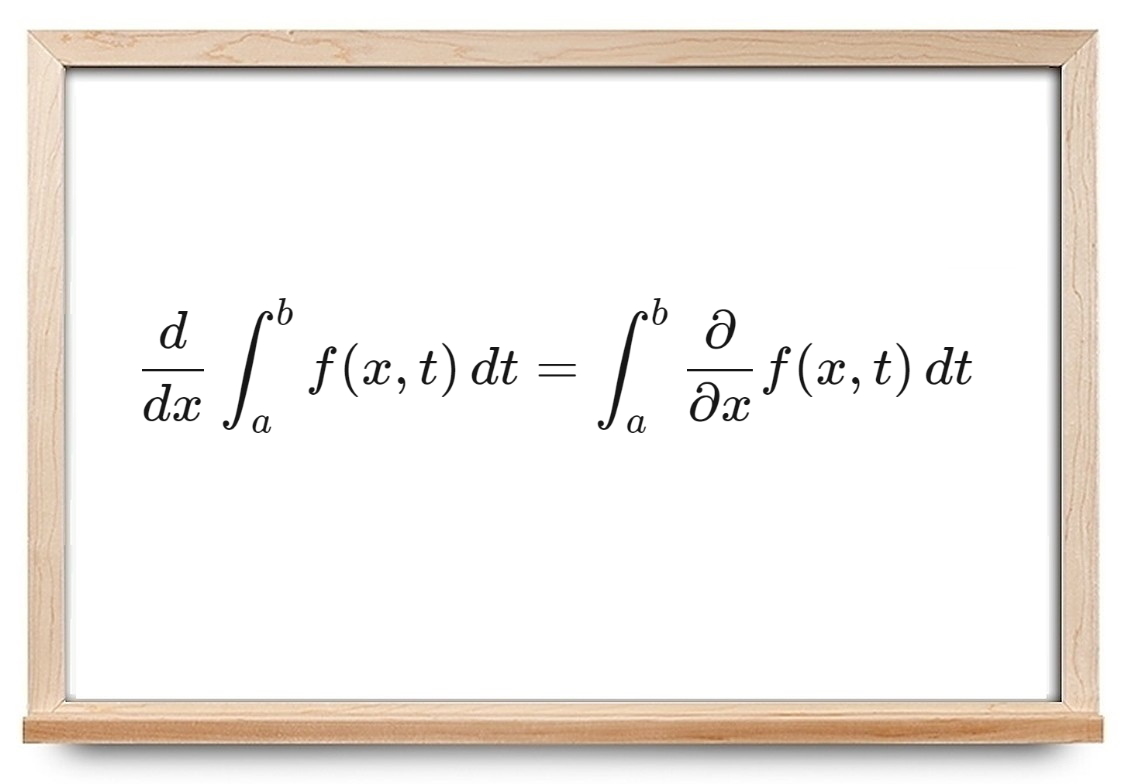
مشتق‌گیری از انتگرال عملیاتی در حسابان است که برای محاسبه برخی انتگرال‌ها استفاده می‌شود. مشتق انتگرال این امکان را می‌دهد تا مرتبه انتگرال‌گیری و مشتق‌گیری را تغییر دهیم.

در ساده‌ترین شکل این کار، به نام «قانون انتگرال لایبنیتس» (Leibniz Integral Rule)، مشتق از انتگرال منجر به معادله زیر می‌شود:

$$ \large \frac { d } { d x } \int _ { a } ^ { b } f ( x , t ) \, d t = \int _ { a } ^ { b } \frac { \partial } { \partial x } f ( x , t ) \, d t . $$

بسیاری از انتگرال‌ها که حل آن‌ها دشوار است یا به روش‌های پیچیده‌ای برای حل نیاز دارند، با این روش قابل حل هستند.

فرم کلی مشتق انتگرال

عمومی‌ترین فرم مشتق انتگرال این‌گونه است: اگر $$ f ( x , t ) $$ یک تابع پیوسته و مشتق‌پذیر پیوسته باشد (یعنی مشتقات جزئی آن وجود دارند و خود پیوسته‌اند) و حدود انتگرال‌گیری $$ a ( x ) $$ و $$ b ( x ) $$ توابعی پیوسته و مشتق‌پذیر پیوسته از $$ x $$ باشند، آنگاه داریم:

$$ \large \frac { \mathrm { d } } { \mathrm { d } x } \int _ { a ( x ) } ^ { b ( x ) } f ( x , t ) \, \mathrm { d } t = f ( x , b ( x ) ) \cdot b' ( x ) - f ( x , a ( x ) ) \cdot a' ( x ) + \int _ { a ( x ) } ^ { b ( x ) } \frac { \partial } { \partial x } f ( x , t ) \, \mathrm { d } t . $$

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

برای مواردی که $$ a ( x ) $$ و $$ b ( x ) $$ توابع ثابتی باشند، فرمول ساده زیر را خواهیم داشت:

$$ \large \frac { \mathrm { d } } { \mathrm { d } x } \int _ { a } ^ { b } f ( x , t ) \,\mathrm { d } t = \int _ { a } ^ { b } \frac { \partial } { \partial x } f ( x , t ) \, \mathrm { d } t . $$

اثبات فرمول مشتق انتگرال

اثبات فرمول مشتق انتگرال را برای حالتی بیان می‌کنیم که حدود ثابت و برابر با $$ a $$ و $$ b $$ باشند. از قضیه فوبینی برای تغییر مرتبه انتگرال‌گیری استفاده می‌کنیم. برای هر $$ x $$ و $$ h > 0 $$، هم $$ x $$ و هم $$ x + h $$ در بازه $$[x_0,x_1]$$ قرار دارند. به گونه‌ای که داریم:

$$ \large \begin {align*} \int _ x ^ { x + h } \int _ a ^ b f _ x ( x , t ) \, d t \, d x & = \int_a^b \int_x^{x+h} f_x(x,t) \,dx \,dt \\& = \int_a^b \left(f(x+h,t)-f(x,t)\right) \,dt \\ &= \int_a^b f(x+h,t) \,dt - \int_a^b f(x,t) \,dt \end {align*} $$

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

توجه کنید از آنجا که $$ f _x (x,t)$$ در مستطیل بسته $$[x_0,x_1]*[a,b]$$ بسته است و همچنین پیوسته یکنواخت است، انتگرال‌ها خوش‌تعریف هستند. بنابراین، انتگرال‌های با $$ d t $$ یا $$dx $$ در متغیر دیگر پیوسته هستند و همچنین انتگرال‌پذیر. بنابراین، داریم:

$$ \large \begin{align*} \frac{\int_a^b f(x+h,t) \,dt - \int_a^b f(x,t) \,dt }{h} & = \frac{1}{h}\int_x^{x+h} \int_a^b f_x(x,t) \,dt \,dx \\ & = \frac{F(x+h)-F(x)}{h} \end {align*} $$

که در آن:

$$ \large F(u) \equiv \int_{x_0}^{u} \int_a^b f_x(x,t) \,dt \,dx $$

$$F$$ مشتق‌پذیر و مشتق آن $$ \int_a^b f_x(x,t) \,dt $$ است. بنابراین، می‌توانیم حد $$h$$ به سمت صفر را بگیریم. برای سمت چپ این حد برابر است با:

$$ \large \frac{d}{dx}\int_a^b f(x,t) $$

و برای سمت راست داریم:

$$ \large F'(u) = \int_a^b f_x(x,t) \,dt $$

بنابراین، اثبات مورد نظر حاصل می‌شود:

$$ \large \frac{d}{dx}\int_a^b f(x,t) = \int_a^b f_x(x,t) $$

در صورت علاقه به یادگیری روش‌های تعیین مشتق توابع مختلف، مطالعه مطلب «فرمول‌های مشتق مهم + سوال با جواب و دانلود PDF» را به شما پیشنهاد می‌کنیم.

مثال‌هایی از مشتق انتگرال

به طور کلی، از مشتق انتگرال برای محاسبه انتگرال‌هایی استفاده می‌کنیم که متعلق به برخی از خانواده‌های انتگرال‌های پارامتری شده با یک متغیر حقیقی هستند. برای درک بهتر این موضوع، مثال زیر را در نظر بگیرید.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

مثال اول مشتق انتگرال

انتگرال معین زیر را محاسبه کنید.

$$ \large \int _ { 0 } ^ { 1 } \frac { t ^ { 3 } - 1 } { \ln t } \, d t . $$

حل: به نظر می‌رسد که این انتگرال را نمی‌توان با تکنیک‌های استاندارد انتگرال‌گیری، مانند جزء به جزء، تغییر متغیر و... حل کرد. بنابراین، آن را با مشتق‌گیری از انتگرال حل می‌کنیم.

اما برای استفاده از روش مشتق انتگرال باید چه تابعی را انتخاب کنیم؟ حضور $$ \ln t $$ در مخرج انتگرالده کاملاً نامطلوب است و باید از دست آن خلاص شویم. تساوی زیر را از دانسته‌های قبلی خود می‌دانیم:

$$ \large \frac { d } { d x } t ^ x = t ^ x \ln t , $$

بنابراین، مشتق صورت نسبت به نما آن چیزی است که می‌خواهیم انجام دهیم.

بدین منظور، تابع زیر را تعریف می‌کنیم:

$$ \large g ( x ) = \int _ { 0 } ^ { 1 } \frac { t ^ x - 1 } { \ln t } \, d t . $$

در این نمادگذاری، انتگرالی که باید محاسبه کنیم، $$ g ( 3 ) $$ است. توجه کنید که انتگرال داده شده، خانواده‌هایی که انتگرال‌های $$ g ( x ) $$ را تعریف می‌کند که با متغیر $$x$$ مشخص شده‌اند.

طبق فرمول انتگرال لایبنیتس، عبارت زیر را محاسبه می‌کنیم:

$$ \large g' ( x ) = \int _ { 0 } ^ { 1 } \frac { \partial } { \partial x } \frac { t ^ x - 1 } { \ln t } \, d t = \int _ { 0 } ^ { 1 } \frac { t ^ x \ln t } { \ln t } \, d t = \frac { t ^ { x + 1 } } { x + 1 } \Bigg \vert _ { 0 } ^ { 1 } = \frac { 1 } { x + 1 } . $$

در نتیجه، $$ g ( x ) = \ln |x + 1 | + C $$ را برای عدد ثابت $$ C $$ خواهیم داشت.

برای مشخص کردن $$ C $$ از $$ g (0) = 0 $$ کمک می‌گیریم، بنابراین، $$ 0 = g ( 0 ) = \ln 1 + C = C $$. در نتیجه، $$ g ( x ) = \ln |x + 1 | $$ را برای همه $$ x $$ها داریم، به گونه‌ای که انتگرال وجود داشته باشد. به طور خاص، $$ g ( 3 ) = \ln 4 = 2 \ln 2 $$.

در مثال بالا، بخشی از انتگرالده با یک متغیر جایگزین شد و تابع حاصل با استفاده از مشتق انتگرال مورد مطالعه قرار گرفت. این مثال یک تصویر خوب از اصل حل مسئله است: اگر در یک مسئله خاص گیر کرده‌اید و به مشکل برخورده‌اید، یک مسئله کلی‌تر را حل کنید.

مثال زیر کارایی فرم عمومی این روش را برای انتگرال گاوسی نشان می‌دهد.

مثال دوم مشتق انتگرال

انتگرال معین زیر را حل کنید.

$$ \large \int _ { 0 } ^ { \infty } e ^ { - x ^ 2 / 2 } \, d x . $$

حل: تابع زیر را تعریف می‌کنیم:

$$ \large g ( t ) = \left ( \int _ { 0 } ^ { t } e ^ { - x ^ 2 / 2 } \, d x \right ) ^ 2 . $$

هدف محاسبه $$ g ( \infty ) $$ و سپس ریشه دوم آن است.

با مشتق‌گیری نسبت به $$ t$$، داریم:

$$ \large \begin {align*} g' ( t ) & = 2 \cdot \left ( \int _ { 0 } ^ { t } e ^ { - x ^ 2 / 2 } \, d x \right ) \cdot \left ( \frac { d } { d t } \int _ { 0 } ^ { t } e ^ { - x ^ 2 / 2 } \, d x \right ) \\ & = 2 e ^ { - t ^ 2 / 2 } \int _ { 0 } ^ { t } e ^ { - x ^ 2 / 2 } \, d x = 2 \int _ { 0 } ^ { t } e ^ { - ( t ^ 2 + x ^ 2 ) / 2 } \, d x . \end {align*} $$

از تغییر متغیر $$ u = x / t $$ استفاده می‌کنیم و انتگرال را به صورت زیر می‌نویسیم:

$$ \large g' ( t ) = 2 \int _ { 0 } ^ { 1 } t e ^ { - ( 1 + u ^ 2 ) t ^ 2 / 2 } \, d u . $$

اکنون انتگرالده یک پادمشتق به فرم بسته نسبت به $$ t $$ دارد:

$$ \large g' ( t ) = - 2 \int _ { 0 } ^ { 1 } \frac { \partial }{ \partial t } \frac { e ^ { - ( 1 + u ^ 2 ) t ^ 2 / 2 } } { 1 + u ^ 2 } \, d u = - 2 \frac { d } { d t } \int _ { 0 } ^ { 1 } \frac { e ^ { - ( 1 + u ^ 2 ) t ^ 2 / 2 } } { 1 + u ^ 2 } \, d u . $$

عبارت زیر را تعریف می‌کنیم:

$$ \large h ( t ) = \int _ { 0 } ^ { 1 } \frac { e ^ { - ( 1 + x ^ 2 ) t ^ 2 / 2 } } { 1 + x ^ 2 } \, d x . $$

با محاسبات بالا، $$ g' ( t ) = - 2 h' ( t) $$ و در نتیجه، $$ g ( t ) = - 2 h ( t) + C $$ است. برای تعیین $$ C$$، مقدار $$ t $$ را در معادله به صفر میل می‌دهیم. از آنجا که $$ g ( 0 ) = 0 $$ و

$$ \large h ( 0 ) = \int _ { 0 } ^ { 1 } \frac { 1 } { 1 + x ^ 2 } \, d x = \tan ^ { - 1 } x \Bigg \vert _ { 0 } ^ { 1 } = \frac { \pi } { 4 } , $$

خواهیم داشت:

$$ \large 0 = -\pi/2 + C \implies C = \pi/2 $$

در نهایت، با $$ t \to \infty $$، داریم: $$ g(\infty) = -2h(\infty) + \pi/2 = \pi/2 $$. در نتیجه، جواب نهایی برابر است با:

$$ \large \int _ { 0 } ^ { \infty } e ^ { - x ^ 2 / 2 } \, d x = \sqrt { \small\pi / 2 } . $$

مثال سوم مشتق انتگرال

فرض کنید $$a$$، $$ b $$ و $$ c > 0 $$ اعدادی حقیقی باشند. تساوی زیر را اثبات کنید:

$$ \large \int _ { - \infty } ^ { \infty } e ^ { - c x ^ { 2 } } \operatorname {erf} ( a x + b ) \, \mathrm { d } x = \sqrt { \frac { \pi } { c } } \operatorname {erf} \left ( \frac { b \sqrt { c } } { \sqrt { a ^ { 2 } + c } } \right ) $$

در عبارت بالا، $$ \mathrm{erf}$$ تابع خطا را نشان می‌دهد.

حل: تساوی زیر را تعریف می‌کنیم:

$$ \large I ( a , b , c ) = \int _ { - \infty } ^ { \infty } e ^ { - c x ^ { 2 } } \operatorname {erf} ( a x + b ) \mathrm { d } x $$

اگر از تغییر متغیر $$ u = \sqrt {c} x $$ استفاده کنیم، به رابطه زیر می‌رسیم:

$$ \large I ( a , b , c ) = \int _ { - \infty } ^ { \infty } e ^ { -u ^ { 2 } } \operatorname {erf} \left ( \frac { a } { \sqrt { c } } u + b \right ) \frac { \mathrm { d } u } { \sqrt { c } } = \frac { 1 } { \sqrt { c } } I \left ( \frac { a } { \sqrt { c } } , b , 1 \right ) $$

بنابراین، بر یافتن $$ J ( a , b ) , I ( a , b , 1 ) $$ تمرکز می‌کنیم. مشتق تابع خطا به صورت زیر است:

$$ \large \operatorname {erf} x = \frac { 2 } { \sqrt { \pi } } \int _ { 0 } ^ { x } e ^ { - t ^ { 2 } } \mathrm { d } t \quad \Longrightarrow \quad \operatorname {erf} ^ { \prime }( x ) = \frac { 2 } { \sqrt { \pi } } e ^ { - x ^ { 2 } } $$

با مشتق‌گیری از انتگرال نسبت به $$ a $$، خواهیم داشت:

$$ \large \frac { \partial J } { \partial a } = \int _ { - \infty } ^ { \infty } e ^ { - x ^ { 2 } } \frac { \partial } { \partial a } \operatorname {erf} ( a x + b ) \mathrm { d } x = \frac { 2 } { \sqrt { \pi } } \int _ { - \infty } ^ { \infty } x e ^ { - x ^ { 2 } } e ^ { - ( a x + b ) ^ { 2} } \mathrm { d } x $$

نمای $$ e $$ را می‌توان به فرم زیر نوشت:

$$ \large x ^ { 2 } + ( a x + b ) ^ { 2 } = \left ( a ^ { 2 } + 1 \right ) x ^ { 2 } + 2 a b x + b ^ { 2 } = \left ( a ^ { 2 } + 1 \right ) \left ( x + \frac { a b }{ a ^ { 2 } + 1 } \right ) ^ { 2 } + \frac { b ^ { 2 } } { a ^ { 2 } + 1 } $$

در نتیجه، مشتق برابر است با:

$$ \large \begin {aligned} \frac { \partial J } { \partial a } & = \frac { 2 } { \sqrt { \pi } } \exp \left ( \frac { - b ^ { 2 } } { a ^ { 2 } + 1 } \right ) \int _ { - \infty } ^ { \infty } x \exp \left [ - \left ( a ^ { 2 } + 1 \right ) \left ( x + \frac { a b }{ a ^ { 2 } + 1 } \right ) ^ { 2 } \right ] \mathrm { d } x \\ & = \frac { 2 } { \sqrt { \pi } } \exp \left ( \frac { - b ^ { 2 } }{ a ^ { 2 } + 1 } \right ) \int _ { - \infty } ^ { \infty } \left ( v - \frac { a b } { a ^ { 2 } + 1 } \right ) \exp \left [ - \left ( a ^ { 2 } + 1 \right ) v ^ { 2 } \right ] \mathrm { d } v \quad \left [ v = x + a b / \left ( a ^ { 2 } + 1 \right ) \right ] \\ & = \frac { 2 }{ \sqrt { \pi } } \left ( - \frac { a b } { a ^ { 2 } + 1 } \right ) \exp \left ( \frac { - b ^ { 2 } } { a ^ { 2 } + 1 } \right ) \int _ { - \infty } ^ { \infty } \exp \left [ - \left ( a ^ { 2 } + 1 \right ) v ^ { 2 } \right ] \mathrm { d } v \quad \left [ \text { using oddness of } v e ^ { - \left ( a ^ { 2 } + 1 \right ) v ^ { 2 } } \right ] \\ & = \frac { 2 } { \sqrt { \pi } } \left ( - \frac { a b } { a ^ { 2 } + 1 } \right ) \exp \left ( \frac { - b ^ { 2 } } { a ^ { 2 } + 1 } \right ) \frac { \sqrt { \pi } } { \sqrt { a ^ { 2 } + 1 } } \quad [ ( i ) ] \\ & = \frac { - 2 a b } { \left ( a ^ { 2 } + 1 \right ) ^ { 3 / 2 } } \exp \left ( \frac { -b ^ { 2 } } { a ^ { 2 } + 1 } \right ) \end {aligned} $$

برای ($$i$$)، داریم:

$$ \large \int _ { - \infty } ^ { \infty } e ^ { - x ^ { 2 } } \mathrm { d } x = \sqrt { \pi } \quad \text { , } \quad \Gamma \left ( \frac { 1 } { 2 } \right ) = \sqrt { \pi } $$

بنابراین، وقتی $$ a \to - \infty$$، آنگاه $$ J ( a , b ) \to 0 $$ و در نهایت، داریم:

$$ \large J ( a , b ) = - 2 b \int _ { - \infty } ^ { a } \frac { x } { \left ( x ^ { 2 } + 1 \right ) ^ { 3 / 2 } } \exp \left ( \frac { - b ^ { 2 } } { x ^{ 2 } + 1 } \right ) \mathrm { d } x $$

از تغییر متغیر $$ u ^ 2 = b ^ 2 / ( 1 + x ^ 2 ) $$ استفاده می‌کنیم و در نتیجه، داریم:

$$ \large 2 u \mathrm { d } u = \frac { - 2 b ^ { 2 } x } { \left ( 1 + x ^ { 2 } \right ) ^ { 2 } } \mathrm { d } x = \frac { 1 } { \sqrt { 1 + x ^ { 2 } } } \frac { - 2 b ^ { 2 } x }{ \left ( 1 + x ^ { 2 } \right ) ^ { 3 / 2 } } \mathrm { d } x = \frac { u } { b } \left ( \frac { - 2 b ^ { 2 } x } { \left ( 1 + x ^ { 2 } \right ) ^ { 3 / 2 } } \mathrm { d } x \right ) $$

و

$$ \large \mathrm { d } u = \frac { - b x \mathrm { d } x }{ \left ( 1 + x ^ { 2 } \right ) ^ { 3 / 2 } } $$

بنابراین، $$ J(a,b)$$ به صورت زیر خواهد بود:

$$ \large J ( a , b ) = 2 \int _ { 0 } ^ { b / \sqrt { 1 + a ^ { 2 } } } \exp \left ( - u ^ { 2 } \right ) \mathrm { d } u = \sqrt { \pi } \operatorname {erf} \left ( \frac { b } { \sqrt { 1 + a ^ { 2 } } } \right ) $$

و تساوی به شکل زیر اثبات می‌شود:

$$ \large \begin {align*} I ( a , b , c ) & = \frac { 1 } { \sqrt { c } } J \left ( \frac { a } { \sqrt { c } } , b \right ) = \sqrt { \frac { \pi } {c } } \operatorname {erf} \left ( \frac { b } { \sqrt { 1 + a ^ { 2 } / c } } \right ) \\ & = \sqrt { \frac { \pi } { c } } \operatorname {erf} \left ( \frac { b \sqrt { c } }{ \sqrt { c + a ^ { 2 } } } \right ) \end {align*} $$

مثال چهارم مشتق انتگرال

البته مثال‌هایی نیز وجود دارند که روش مشتق انتگرال در آن‌ها کاربرد ندارد. برای مثال، فرض کنید می‌خواهیم انتگرال زیر را محاسبه کنیم:

$$ \large \int _ { 0 } ^ { \infty } \frac { \sin x } { x } \, d x $$

با استفاده از تغییر متغیر $$ u = x / t $$ برای $$ t \neq 0 $$، خواهیم داشت:‌

$$ \large \int _ { 0 } ^ { \infty } \frac { \sin x } { x } \, d x = \int _ { 0 } ^ { \infty } \frac { \sin t u } { u } \, d u = g ( t ) . $$

مشتق انتگرال عبارت زیر را نتیجه می‌دهد:

$$ \large 0 = g' ( t ) = \int _ { 0 } ^ { \infty } \cos t u \, d u $$

که بی‌معنی است. مشکل این است که تابع $$ f ( x , t ) = \sin t x / x $$ مشتق‌پذیر پیوسته نیست (به $$ \partial f / \partial t $$ در $$ x = 0 $$ دقت کنید)، که در فرضیات مذکور بالا مورد نیاز بود.

مثال پنجم مشتق انتگرال

انتگرال معین زیر را محاسبه کنید:‌

$$ \large \int _ { 0 } ^ { 2 \pi } e ^ { \cos \theta } \cos ( \sin \theta ) \, d \theta . $$

از تابع زیر کمک بگیرید:

$$ \large f ( t ) = \int _ { 0 } ^ { 2 \pi } e ^ { t \cos \theta } \cos ( t \sin \theta ) \, d \theta $$

حل: با توجه به تابع $$ f $$، می‌توان نوشت:

$$ \large \begin {array} {rcl} t f' ( t ) & = & \displaystyle t \int _ 0 ^ { 2 \pi } e ^ { t \cos \theta } \big [ \cos \theta \cos ( t \sin \theta ) - \sin \theta \sin ( t \sin \theta ) \big ] \, d \theta \\ & = & \displaystyle \int _ 0 ^ { 2 \pi } \frac { \partial } { \partial \theta } \big [ e ^ { t \cos \theta } \sin ( t \sin \theta ) \big ] \, d \theta \\ & = & \Big [ e ^ { t \cos \theta } \sin ( t \sin \theta ) \Big ] _ 0 ^ { 2 \pi } \; = \; 0 \end {array} $$

از آنجا که $$ f ( 0 ) = 2 \pi $$ است، مقدار $$ f ( 1 ) = 2 \pi $$ را داریم.

مثال ششم مشتق انتگرال

انتگرال زیر را محاسبه کنید:

$$ \large \int _ { 0 } ^ { 1 } ( x \ln x ) ^ { 5 0 } \, d x . $$

حل: از روش مشتق انتگرال استفاده می‌کنیم. عبارت زیر را در نظر بگیرید:

$$ \large F ( a ) = \int _ 0 ^ 1 x ^ a \text {dx} = \dfrac { 1 }{ a + 1 } $$

با ۵۰ بار مشتق‌گیری از $$F$$ نسبت به $$ a $$، خواهیم داشت:‌

$$ \large F ^ { ( 5 0 ) } ( a ) = \int _ 0 ^ 1 \ln ^ { 5 0 }( x ) x ^ a \text {dx} = \dfrac { 5 0 ! } { ( a + 1 ) ^ { 5 1 } } $$

جواب مسئله با قرار دادن $$ a = 50 $$ به دست می‌آید:

$$ \large F ^ { ( 50 ) } ( 5 0 ) = \int _ 0 ^ 1 \ln ^ { 5 0 }( x ) x ^ { 5 0 } \text {dx} = \boxed { \dfrac { 5 0 ! } { 5 1 ^ { 5 1 } } } $$