مساحت کره و محاسبه آن | به زبان ساده

«کُره» (Sphere) یک حجم هندسی سه‌بعدی کاملاً گرد است. کره را می‌توان با مجموعه همه نقاطی که در فاصله $$ r $$ (شعاع) از یک نقطه مشخص (مرکز) دارند تعریف کرد. این حجم هندسی کاملاً متقارن است و یال یا رأس ندارد. در این آموزش می‌خواهیم فرمول محاسبه مساحت کره را معرفی کنیم.

فرمول مساحت کره

منظور از مساحت کره، مساحت سطح رویه آن است. کره چند ویژگی جالب دارد و یکی از آن‌ها این است که در میان همه احجام با سطح رویه برابر، کره حجم بیشتری دارد.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

فرمول مساحت کره به صورت زیر بیان می‌شود:

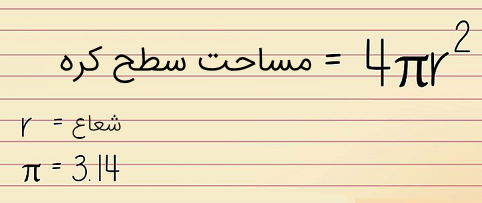
بنابراین، مساحت سطح کره‌ای به شعاع $$r$$ برابر با $$ 4 \pi r ^ 2 $$ است. همچنین، حجم کره $$ \frac 43 \pi r ^ 3 $$ است.

اثبات فرمول مساحت کره

برای اثبات اینکه مساحت سطح کره‌ای به شعاع $$ r $$ برابر با $$ 4 \pi r ^ 2 $$ است، یک راه ساده استفاده از حسابان است.

فیلم آموزش هندسه پایه دهم – هندسه ۱ در فرادرس

کلیک کنید

ابتدا باید به این نکته پی ببریم که برای یک منحنی که با $$ x ( t) $$ و $$ y ( t) $$ پارامتری شده است، طول کمان برابر خواهد بود با:

$$ \large S = \int _ a ^ b \sqrt { \left ( \frac { d y } { d t } \right ) ^ 2 + \left ( \frac { d x } { d t } \right ) ^ 2 } \, d t . $$

با توجه به این رابطه، می‌توانیم فرمول مساحت سطح یک جسم را با دوران منحنی حول محور $$ x $$ به دست آوریم. بنابراین، خواهیم داشت:

$$ \large A = 2 \pi \int _ a ^ b y \sqrt { \left ( \frac { d y } { d t } \right ) ^ 2 + \left ( \frac { d x } { d t } \right ) ^ 2 } \, d t . $$

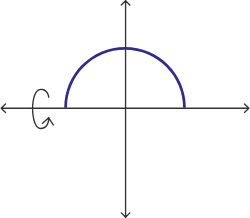
با چرخاندن نیم‌دایره حول محور $$ x $$ می‌توانیم یک کره را ایجاد کنیم. معادلات این نیم‌دایره، $$ x ( t) =  r \cos ( t ) $$ و $$ y ( t) = r \sin ( t) $$ برای $$ 0 \le t \le \pi $$ است. بنابراین، خواهیم داشت:

$$ \large \frac { d x } { d t } = - r \sin ( t ) , \quad \frac { d y } { d t } = r \cos ( t ) . $$

با جایگذاری این روابط در فرمول مساحت سطح، جواب مورد نظر که همان فرمول مساحت کره است، به دست می‌آید:

$$ \large \begin {aligned} A & = 2 \pi \int _ 0 ^ \pi r \sin ( t ) \sqrt { \big ( - r \sin ( t ) \big ) ^ 2 + \big ( r \cos ( t ) \big ) ^ 2 } \ d t \\ & = 2 \pi \int _ 0 ^ \pi r \sin ( t ) \sqrt { r ^ 2 \big ( \sin ( t) ^ 2 + \cos ( t ) ^ 2 \big ) } \ dt \\ & = 2 \pi \int _ 0 ^ \pi r ^ 2 \sin ( t ) \ d t \\ & = 2 \pi r ^ 2 \int _ 0 ^ \pi \sin ( t ) \ d t \\ & = 4 \pi r ^ 2 . \end{aligned} $$

قضیه جعبه کلاه ارشمیدس

قضیه جعبه کلاه ارشمیدس بیان می‌کند که برای هر برش مقطعی کره، مساحت سطح جانبی برابر مساحت سطح جانبی استوانه‌ای با همان ارتفاع و همان شعاع کره است. به عبارت بهتر، در شکل زیر، دو مساحت جانبی $$ S_ 1 $$ و $$ S_ 2 $$ برابرند.

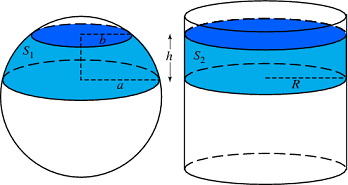
اثبات: از اثبات قبلی استفاده می‌کنیم. پس از دوران نیم‌دایره حول محور $$ x $$، یک سطح کره خواهیم داشت و اگر یک مقطع جزئی را با قاعده مشابه از آن ببریم، مساحت سطح جدید مطابق شکل زیر خواهد بود.

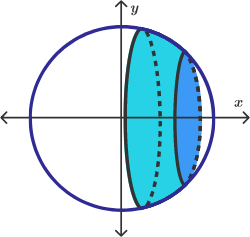
با توجه به شکل بالا، سطح جانبی با رنگ آبی روشن با دو قاعده با شعاع متفاوت نشان داده شده است. برای نمایش بهتر ارتفاع قرص، آن را ۹۰ درجه می‌چرخانیم و به صورت شکل زیر نشان می‌دهیم.

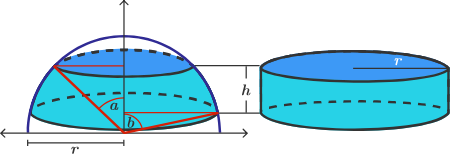
اکنون درون قرص دو متغیر زاویه $$ \angle a $$ و $$ \angle b $$ وجود دارد که به عنوان حدود انتگرال‌گیری آن ظاهر می‌شوند.

مساحت سطح جانبی ($$ A'$$) را می‌توان به صورت زیر محاسبه کرد:

$$ \large \begin {aligned} A' & = 2 \pi r ^ 2 \int _ a ^ b \sin ( t ) \ d t \\ & = 2 \pi r ^ 2 \left [ \left . - \cos ( t ) \right | _ a ^ b \right ] \\ & = ( 2 \pi r ) r \big [ \cos ( a ) - \cos ( b ) \big ] . \end {aligned} $$

با توجه به مثلث‌های قائم‌الزاویه با شعاع $$ r $$ (قرمز ضخیم)، واضح است که $$ r $$ وتر هر دو است. در نتیجه، اضلاع عمود را می‌توان به صورت $$ r \times \cos (a ) $$ و $$ r \times \cos ( b ) $$، به ترتیب، برای مثلث‌های چپ و راست محاسبه کرد.

بنابراین، ارتفاع قرص $$ h = \big ( r \times \cos ( a ) \big ) - \big ( r \times \cos ( b ) \big ) = r \big [ \cos ( a ) - \cos ( b ) \big ] $$ خواهد بود. با جایگذاری این جمله در معادله قبلی، خواهیم داشت:

$$ \large A' = ( 2 \pi r ) r \big [ \cos ( a ) - \cos ( b ) \big ] = 2 \pi r h . $$

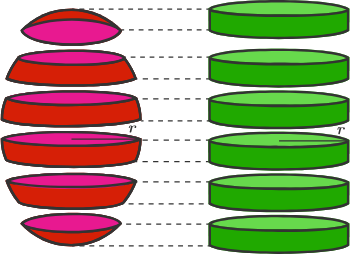
واضح است که این فرمول برای سطح جانبی استوانه‌ای به شعاع $$ r $$ و ارتفاع $$ h $$ نیز وجود دارد. این بدین معنی است که مساحت سطح جانبی یک برش قرصی از کره برابر با مساحت سطح جانبی استوانه‌ای به شعاع $$ r $$ و ارتفاع $$ h $$ است و این گفته برای هر سطحی از کره صحیح است.

مثال‌های محاسبه مساحت کره

در این بخش، چند مثال را از محاسبه مساحت کره ارائه می‌کنیم.

فیلم آموزش هندسه پایه دهم – هندسه ۱ در فرادرس

کلیک کنید

مثال ۱: مساحت سطح یک کره با شعاع ۳ را به دست آورید.

حل: با توجه به فرمولی که گفتیم، مساحت سطح کره برابر خواهد بود با:

$$ \large A = 4 \pi \times r ^ 2 = 4 \pi \times 3 ^ 2 = 3 6 \pi$$

مثال ۲: اگر حجم کره‌ای $$ 36 \pi $$ باشد، مساحت سطح آن چقدر است؟

حل: حجم کره را می‌توان به صورت زیر نوشت:

$$ \large 3 6 \pi = \frac { 4 } { 3 } \pi \times 3 ^ 3 . $$

از آنجا که حجم یک کره با شعاع $$ r $$ برابر با $$\frac 43 \pi r ^ 3 $$ است، در می‌یابیم که شعاع کره برابر با $$ r = 3 $$ خواهد بود. بنابراین، با توجه به فرمولی که پیش‌تر ارائه کردیم، مساحت سطح کره به صورت زیر محاسبه می‌شود:

$$ \large 4 \pi r ^ 2 = 4 \pi \times 3 ^ 2 = 3 6 \pi . $$

مثال ۳: حجم یک کره ۸ برابر شده است. مساحت سطح آن چند برابر شده؟

حل: می‌دانیم که حجم کره برابر با $$ \frac 43 \pi r ^ 3 $$ است. این نتیجه می‌دهد که حجم با $$ r ^ 3 $$ متناسب است و می‌توان نوشت: $$ \frac { 4 } { 3 } \pi r ^ 3 \propto r ^ 3 $$. این یعنی ۸ برابر شدن حجم به معنی ۲ برابر شدن شعاع است. در نتیجه، از آنجا که مساحت سطح کره متناسب با $$ r ^ 2 $$ است، یعنی $$ 4 \pi r^2 \propto r^2 $$، می‌توانیم بگوییم مساحت سطح کره $$ 2 ^ 2 = 4 $$ برابر شده است.

مثال ۴: هندوانه‌ای داریم که حجم کل آن ۲۸۸ سانتی‌متر مکعب است. اگر آن را به دو قسمت تقسیم کنیم، مساحت سطح هر نصف هندوانه چقدر است؟ (فرض کنید هندوانه یک کره کامل است).

حل: با توجه به فرمول $$ V = \frac 43 \pi r ^ 3 $$ برای حجم یک کره به شعاع $$ r $$، در می‌یابیم که شعاع هندوانه $$ r = 6 $$ سانتی‌متر است. از آنجا که هندوانه را دقیقاً نصف کرده‌ایم، شاید بگویید که مساحت سطح نصف هندوانه، دقیقاً برابر با نصف مساحت سطح کل آن است. اما این گفته صحیح نیست.

همان‌طور که در شکل بالا می‌بینیم، مساحت سطح نصف هندوانه به اندازه سطح $$A$$ بزرگ‌تر از نصف مساحت سطح هندوانه کامل است. بنابراین، مساحت سطح نصف هندوانه برابر است با:

$$ \large \frac { 1 } { 2 } \times 4 \pi \times 6 ^ 2 + \pi \times 6 ^ 2 = 1 0 8 \pi . $$