مسئله منشی و تصمیم بهینه | به زبان ساده

مسئله منشی معمای مشهوری در حوزه تصمیم و احتمال همچنین بهینهسازی است. هدف از طرح این مسئله، پیدا کردن بهترین استراتژی در زمانی است که دنبالهای از انتخابها وجود داشته و باید از بین آنها بهترین را انتخاب کنیم. این مسئله در اواخر دهه ۵۰ و ۶۰ میلادی ظاهر شد و تبدیل به یک بازی فکری برای ریاضیدانان و آمارشناسان گردید. به دلیل اهمیت این موضوع، همچنین ترکیب مسائل احتمال با بهینه کردن یک تابع، مسئله منشی و تصمیم بهینه را مبنای این متن از مجله فرادرس قرار دادهایم.
برای آشنایی بیشتر با نظریه تصمیم و همچنین مباحث مربوط به نظریه بازیها، بهتر است نوشتارهای نظریه بازی ها و قواعد تصمیم – مفاهیم اولیه و مارتینگل — معرفی و کاربردها را مطالعه کنید. از طرفی خواندن نوشتارهای نظریه احتمال و کاربردهای آن — به زبان ساده و احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه نیز خالی از لطف نیست.
مسئله منشی و تصمیم بهینه
مسئله منشی مربوط به انتخاب یا تصمیم در شرایط بدون اطمینان یا تصادفی است. در نتیجه با احتمال و بخصوص احتمال شرطی در نظریه احتمال سروکار داریم. از طرفی براساس شرایط مسئله به دنبال بهترین تصمیم میگردیم. پس مسئله یک موضوع بهینهسازی نیز هست. فرمولبندی و ادغام شرطهای مسئله باعث ایجاد یک الگو برای حل مسائلی از این نوع خواهد شد که به زبان ریاضی بیان شده و قابل حل هستند. ابتدا خود مسئله منشی و تصمیم بهینه را در موقعیت مشخص، ذکر کرده و شرطهای مربوطه را بیان میکنیم.
فرض کنید که شما مدیر منابع انسانی یک شرکت هستید و باید از بین تعداد مشخصی از درخواستکنندگان موقعیت شغلی، بهترین منشی را استخدام کنید. این کار را میتوانید به صورت انتخاب تصادفی از بین همه افرادی که مصاحبه شدهاند انجام دهید. ولی در این صورت شاید بهترین فرد برای کار شما انتخاب نشود.
شرایط مسئله منشی و تصمیم بهینه نیز مقداری پیچیده است. برای مثال، تصمیم گیری در مورد قبول یا رد یک متقاضی خاص باید بلافاصله پس از مصاحبه انجام شود. اگر کسی قبل از پایان، پذیرفته نشده باشد، آخرین داوطلب انتخاب میشود. بنابراین سوال این است که از چه راهکاری برای به حداکثر رساندن شانس استخدام بهترین متقاضی لازم است؟
در نگاه اول، این موضوع شاید غیرممکن به نظر برسد. در حقیقت، مسئله منشی یک راه حل زیبا بر اساس ریاضیات دارد. میتوان با توجه به شرایط تصادفی حضور متقاضیهای شغل را یک مسئله احتمالی در نظر گرفت. بنابراین باید ریشههای حل آن را در کتابهای ریاضی و احتمال جستجو کرد. شایان ذکر است که بسیاری از مسائلی که روزانه با آنها مواجه هستیم، با مسئله منشی و نظریه تصمیم آماری مشابهت داشته و از طریق شیوه ارائه شده، قابل حل هستند. برای مثال به موضوعات زیر توجه کنید.
- تصمیم گیری برای خرید یا اجاره یک آپارتمان در یک شهر شلوغ (با تعداد خانههای قابل ارائه فراوان).
- یافتن ارزانترین فروشگاه در خیابان پر از مغازه (بدون رفت و برگشت).
- انتخاب و تعهد به یک شریک در یک دوره طولانی مدت (توجه داشته باشید: مسئله منشی را گاهی مسئله ازدواج نیز میشناسند).
- پیدا کردن بهترین موقعیت شغلی از بین شغلهای مشابه.
در همه این موارد، شما نمیدانید که گزینه یا گزینههای بعدی چه هستند. همین موضوع کار را مشکل کرده و به یک مسئله تبدیل میکند. با این حال، لازم است سریع (قبل از انجام مصاحبه از همه داوطلبان) اما به طور صحیح تصمیم بگیرید. هدف این نوشتار نمایش راه حل مسئله منشی در نظریه تصمیم آماری با توجه به فرمولبندی و استفاده از روشهای بهینهسازی ریاضیاتی است.
بیان مسئله استخدام منشی و تصمیم بهینه
مسئله انتخاب منشی و تصمیم بهینه در نسخههای مختلف و متعددی بیان شده است. ولی شرایطی که در مسئله استاندارد آن مطرح شده، به صورت زیر نوشته میشود.
- در این مسئله، فقط یک موقعیت شغلی وجود دارد.
- تعداد شرکتکنندگان برای مصاحبه برابر با $$N$$ است که مقدار آن هنگام انجام مصاحبهها از قبل مشخص است.
- بدون هیچ ابهامی، شرکت کنندگان را طی مصاحبه میتوان رتبهبندی کرد، بطوری که هیچکدام دارای رتبه یکسانی نباشند.
- با توجه به رتبه بندیهای صورت گرفته تا زمان مصاحبه جاری، امکان مقایسه و تصمیمگیری برای گزینه مناسب تا این زمان وجود دارد.
- متقاضیان به شکل تصادفی برای مصاحبه وارد میشوند.
- متقاضی رد شده در مصاحبه مجدد، مصاحبه نمیشود.
- مدیریت تا پیدا کردن بهترین منشی، مصاحبه را ادامه میدهد.
نکته: معیارهای مدیریت و تعیین بهترین فرد، در این مسئله مورد بحث نیست، بلکه فقط رتبهها و مرتبسازی آنها دخیل خواهد بود.
به این ترتیب فقط کسی از میان مصاحبه شدههای قبلی، به عنوان گزینه مناسب انتخاب میشود که از همه کاندیدهای گذشته بهتر باشد. در اینجا مشخص است که گزینههای قبلی همگی مردود شدهاند.
احتمال و تصادفی بودن در مسئله منشی و تصمیم بهینه
واضح است که مسئله منشی و تصمیم بهینه بسیار چالش برانگیز است زیرا شما نمیتوانید در هر مرحله یا مقطع از روند مصاحبه، بهترین متقاضی را مشخص کنید. شاید نفر بعدی بهتر از نفر فعلی باشد. البته مقایسه با نفرات قبلی از پیشفرضهایی است که در این مسئله مورد توجه قرار میگیرد. به این ترتیب میتوانید امتیاز نفر مصاحبه شده را با نفرات قبلی مقایسه کنید.
در مقابل این عدم اطمینان و ناتوانی در گرفتن تصمیم قطعی، یک استراتژی جالب نیز وجود دارد. یک استراتژی میتواند انتخاب تصادفی باشد. به این معنی که این امکان نیز وجود دارد که همه چیز را به شانس و تقدیر واگذار کنید. حتی ممکن است بخواهید که خودسرانه تصمیمی را (بدون توجه به شرایط مصاحبه شونده) عملی کرده و نفر اول (یا آخر) را به عنوان بهترین گزینه انتخاب کنید. جای تعجب نیست که این استراتژیهای تصادفی یا غیر عقلانی، حتما عملکرد ضعیفی خواهند داشت و جواب بهینه را به شما نمیدهند.
این موضوع را در نظر بگیرید که با دیدگاه احتمالی، اگر $$N$$ تعداد کل متقاضیان باشد، با احتمال $$p = \frac{1}{N}$$، نفر اول، بهترین گزینه برای شغل منشیگری خواهد بود. همین امر هنگام انتخاب آخرین داوطلب نیز برقرار است. به این ترتیب احتمال انتخاب نفر $$i$$ام نیز در این بین برابر است با $$p = \frac{1}{N}$$. این احتمال را براساس شانس و تصادف بدست آوردهایم. زیرا با فرض این که نفر $$i$$ بهترین فرد در بین $$N$$ نفر باشد، احتمال انتخاب آن به صورت نسبت دو ترکیب زیر حاصل میشود. به یاد دارید که تعبیر احتمال براساس فراوانی، تعداد حالتهای مطلوب به کل حالتها است. بنابراین داریم:
$$ \large p = \dfrac{ { 1 \choose 1} }{{ N \choose 1 }} = \dfrac{1}{N} $$
بنابراین اگر $$N=3$$ باشد، آنگاه احتمال بهترین انتخاب حدود ۳۳٪ است. همچنین برای $$N=10$$، این احتمال برابر با ۰٫۱ خواهد بود. بنابراین با بیشتر شدن شرکت کنندگان برای مصاحبه شغلی، احتمال انتخاب فرد اصلح، کم و کمتر خواهد شد. پس به نظر میرسد که استراتژی انتخاب تصادفی، رویکرد مناسبی نخواهد بود.
حال زمانی را در نظر بگیرید که تعداد متقاضیان زیاد بوده و $$N$$ بزرگ و بزرگتر شود. معمولا در چنین وضعی میگوییم که $$N$$ به سمت بینهایت میل کرده است. به این ترتیب با این استراتژی، شانس انتخاب فرد مناسب برای سمت منشیگری تقریبا به صفر نزدیک شده، پس هیچگاه چنین فردی را پیدا نخواهیم کرد.
تغییر استراتژی در مسئله منشی و انتخاب بهینه
این بار سعی میکنیم، استراتژی تصادفی را تعدیل کنیم و کمی عقلانیتر عمل کنیم. تا اینجا شاید متوجه شده باشید که تنها متغیری کنترلی که در کل روند مصاحبه با آن روبرو هستید، احتمال رد شدن افراد است.
یک استراتژی میتواند مشخص کردن تعداد افرادی باشد که تا انتخاب شخص مورد نظر، باید در مصاحبه رد شوند. در این صورت باید زمانی طولانی را بسته به این مقدار، طی کنید تا شخص مورد نظرتان پیدا شود. مشخص است که نفر بعدی، با توجه به تعداد افراد رد شده، به ناچار گزینه مناسب شما خواهد بود.
الگوریتم این استراتژی به صورت زیر نوشته شده است:
- با $$R$$ فرد مصاحبه شده و همه آنها رد میشوند. توجه داشته باشید که در بین آنها، چه کسی بالاترین امتیاز را کسب کرده است. نمره یا امتیاز این فرد را به عنوان مرجع، $$Xref$$ مینامیم.
- مصاحبه با متقاضیان بعدی را ادامه دهید تا زمانی که اولین نفر را با نمره بالاتر از Xref پیدا کنیم. یعنی در این حالت داریم $$X > Xref$$، پس او کاندید برای موقعیت شغلی خواهد بود.
این استراتژی نسبت به استراتژی قبلی بهتر و امیدوار کننده به نظر می رسد اما هنوز کامل نشده است: شما باید مقدار $$R$$ یعنی تعداد افراد برای رد کردن را تعیین کنید. در حقیقت سوال این است که بهترین عدد برای $$R$$ کدام مقدار ۱ تا $$N$$ خواهد بود.
اگر مقدار $$R$$ بیش از حد بزرگ باشد، یک روش ارزیابی کامل انتخاب شده است ولی در این بین ممکن است بهترین نامزد را که در گروه افراد پیشین قرار داشته، رد کرده باشید. اگر مقدار $$R$$ خیلی کوچک باشد، شما یک نقطه مرجع نامناسب خواهید داشت و احتمالاً یک نامزد غیربهینه را انتخاب خواهید کرد.
آنچه ما باید انجام دهیم یافتن مقدار مطلوب برای $$R$$ است که آن را $$R^*$$ مینامیم. به منظور تعیین این مقدار کمی از ریاضیات و احتمال شرطی کمک میگیریم. اما قبل از شروع با رویکرد ریاضیات و احتمال، با یک مثال، نحوه کار را روشنتر میکنیم.
آزمایش استراتژی گفته شده را به ازای $$N=3$$ در نظر بگیرید. در اینجا، تنها مقداری که برای $$R$$ وجود دارد مقدار ۱ است. در غیر اینصورت دیگر انتخابی وجود نداشته و شما حتما نفر سوم را به ازاء $$R=2$$ برای موقعیت شغلی و به عنوان انتخاب بهینه، استخدام میکنید. اگر $$R=0$$ باشد، نفر اول را انتخاب خواهید کرد.
به جدول زیر توجه کنید، ۶ حالت مختلف با توجه به انتخاب $$R=1$$ در نظر گرفته شده و نتیجه انتخاب بهینه نیز در ستون آخر دیده میشود. تعداد حالتهایی که بهترین گزینه پاسخ استراتژی (موفق) است با گزینههای شکست، برابر است و شانس پیدا کردن پاسخ بهینه، در این حالت ۵۰-۵۰ است که مسلما از ۳۳٪ که پاسخ مربوط به وضعیت کاملا تصادفی بود، بهتر است.
توجه داشته باشید که هر سطر نشانگر یک سناریو است. خانههای به رنگ بنفش نشانگر گزینه انتخابی و خانهها با رنگ خاکستری نیز موقعیت مردود شدن در مصاحبه را نشان میدهند. خانههای جدول که با زمینه سفید رنگ دیده میشوند نیز نشانگر عدم مصاحبه از فرد مورد نظر هستند.
| کاندید ۱ (همیشه مردود) | کاندید ۲ | کاندید ۳ | نتیجه اجرای استراتژی |
| ضعیف | متوسط | عالی | شکست |
| ضعیف | عالی | متوسط | موفق |
| متوسط | ضعیف | عالی | موفق |
| متوسط | عالی | ضعیف | موفق |
| عالی | متوسط | ضعیف | شکست |
| عالی | ضعیف | متوسط | شکست |
استراتژی کامل برای مسئله منشی و تصمیم بهینه
ابتدا باید احتمال موفقیت یا همان $$P(R)$$ در انتخاب بهترین نامزد برای مقادیر مختلف $$R$$ فرمولبندی کرده، سپس این فرمول را به ازاء مقدار $$R$$، بیشینه کنیم. احتمال موفقیت را میتوان مجموع احتمالات یافتن بهترین نامزد در موقعیت n دانست، جایی که n را میتوان بین $$R + 1$$ و کل نفرات $$N$$ مشخص نمود. واضح است که این نفرات همان نامزدهای باقی مانده از حذف $$R$$ متقاضی مصاحبه شده هستند. ابتدا پیشامدهای احتمالی زیر را تعریف میکنیم.
- $$R$$: پیشامد انتخاب بهترین گزینه بعد از حذف $$R$$ مصاحبه شونده
- $$A_n$$ : پیشامد انتخاب $$n$$امین نفر
- $$B_n$$: پیشامد بهترین گزینه بودن نفر $$n$$ام
حال رابطههای زیر را براساس احتمال شرطی خواهیم داشت.
$$ \large P(R) = \sum_{n = R + 1 }^N P(A_n \cap B_n) $$
به یاد دارید که قبول یک کاندید برای شغل منشیگری، فقط بستگی به این دارد که امتیازش از $$R$$ نفر قبلی بیشتر باشد ولی این امر به معنی بهینه بودن جواب نیست. واضح است که احتمال مورد نظر به مقدار $$R$$ بستگی داشته و به عنوان پارامتر تابع احتمال در فرمول بالا به کار رفته است.
برای محاسبه این احتمال دو شیوه یا راه حل را در نظر میگیریم. در حالت اول فرض بر این است که گزینه برتر دوم را رد کردهایم. در حالت دوم نیز قید یا شرطی روی مصاحبه شوندگان میگذاریم. به این معنی که همه افراد از $$R+1$$ تا $$N$$ مورد بررسی قرار میگیرند.
روش اول در محاسبه احتمال برای کاندید $$n$$ام
فرض بر این است که در بین $$N$$ مصاحبه شونده، بهترین کاندید شغلی نفر $$n$$ام است که در بین نفرات $$R+1$$ تا $$N$$ قرار دارد. واضح است که در این صورت، نفر برتر دیگری نیز وجود داشته که از نفر $$n$$ام، امتیاز کمتری دریافت کرده. او را در مسئله منشی و تصمیم بهینه به نام کاندید دوم معرفی میکنیم. کاندید دوم باید در میان نفرات اول تا $$R$$ام قرار گرفته باشد. معنی این عبارات این است که نحوه ارزیابی ما مصاحبه را به شکلی تنظیم کرده که همه را به جز یک نفر برحسب امتیاز دریافتی، مردود خواهد کرد.
برای روشن شدن موضوع به تصویر زیر توجه کنید. فرض بر این است که نفر $$n$$ام بهترین کاندید بوده و کاندید دوم نیز مردود شده است.
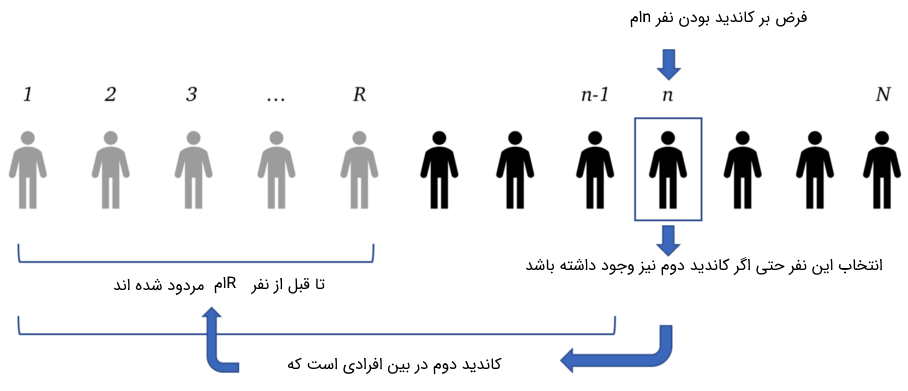
این تصویر را به بیان ریاضی به صورت زیر خواهیم نوشت:
- $$C_R$$: پیشامد کاندید دوم در بین همه $$n-1$$ مصاحبه شوند در گروه $$R$$ نفر اول قرار گرفته است.
$$ \large P(R) = \sum_{n= R+1}^N P( A_n \cap B_n) = \sum_{n= R+1}^N P(B_n) P(C_R) \\ \large \sum_{n= R+1}^N \dfrac{1} {N} \dfrac{R} {n-1} = \dfrac{R} {N} \sum_{n= R+1}^N \dfrac{1} {n-1} $$
روش دوم با فرض رد شدن نفرات قبلی در محاسبه احتمال برای کاندید $$n$$ام
روش دیگر برای انتخاب نفر $$n$$ام و کاندید بودن او بر این فرض استوار است که همه نفرات قبلی از $$R+1$$ تا $$N$$ دارای امتیاز کمتری نسبت به نفر $$n$$ام هستند. به منظور انتخاب و ارزیابی هر یک از این نفرات در مسئله منشی و تصمیم بهینه نیز از پرتاب سکه استفاده میکنیم.
نتیجه پرتاب سکه مشخص میکند که آیا این کاندید بهترین امتیاز را کسب میکند. از آنجایی که ترتیبها تصادفی هستند، احتمال بدست آوردن بهترین رکورد برابر با $$\frac{1}{m}$$ است که در آن $$m$$ موقعیت کاندید جاری است.
پس باید همه پرتابهای سکه برای نفرات غیر از $$m$$امین فرد، همراه با شکست باشد. به این ترتیب احتمال اینکه نتیجه سکه برای نفر $$n$$ام موفقیت باشد برابر است با $$1-\frac{1}{m}$$. به این ترتیب فرمولها را به صورت زیر مینویسیم:
$$ \large P(R) = \sum_{n =R+1}^N P( B_n \cap B'_m) = \\ \large \sum_{n =R+1}^N \dfrac{1}{n} \prod_{m = R+1 , \ldots, N , m \neq n } (1- \dfrac{1}{m}) = \\ \large \prod_{m =R+1,\ldots,N} \left(1- \dfrac{1}{m} \right) \sum_{n= R+1}^N \dfrac{1}{n \left(1 - \dfrac{1}{n} \right) } =\\ \large \dfrac{R}{N} \sum_{n= R+1}^N \dfrac{1}{n-1} $$
واضح است که نتیجه هر دو رویکرد یکسان خواهد بود. حال باید به کمک روشهای بهینه سازی، این احتمال را برحسب $$R$$ بیشینه کنیم.
نکته: توجه دارید که فرمول بالا را به ازای $$R=0$$ محاسبه نخواهیم کرد، زیرا در این صورت مخرج کسر مربوط به جمع، صفر خواهد شد. واضح است که در این صورت احتمال انتخاب نفر $$n$$ام به عنوان فرد برتر برابر با $$\frac{1}{n}$$ است، زیرا هیچ کدام از افراد، در ابتدای مصاحبه کنار گذاشته نشدهاند.
تعیین مقدار $$R$$ در مسئله منشی و تصمیم بهینه
فرمول بالا را در حالتی که $$N$$ به سمت بینهایت میل کند در نظر بگیرید. مقدار $$x$$ را هم در این حالت، حد $$\dfrac{R}{N}$$ محسوب کنید. با استفاده از نمایش $$t$$ به جای $$\frac{n-1}{N}$$ و $$dt=\frac{1}{N}$$، حاصل جمع رابطه بالا را به صورت انتگرال زیر نمایش میدهیم. توجه داشته باشید که $$dt$$ براساس دیفرانسیل برحسب $$n$$ که پارامتر تابع مورد نظر است، صورت گرفته خواهد شد.
$$\large {\displaystyle P(x) = x \int _{x}^{1}{ \frac {1}{t}} \,dt= -x \ln(x) \;} $$
در حقیقت، رابطه زیر را با تقسیم کردن بر $$N$$ و تغییرات لازم به شکل یک انتگرال در آوردهایم.
$$ \large \dfrac{R}{N} \sum_{n= R+1}^N \dfrac{1}{n-1} $$
پس
$$\large \dfrac{N}{n-1} \rightarrow t , \;\;\; n =\dfrac{R+1}{N} \rightarrow x , \;\;\;\;\sum \rightarrow \int$$
همانطور که به یاد دارید، یکی از روشهای بهینهسازی تابع پیوسته، مشتقگیری نسبت به متغیر (در اینجا $$x$$) و پیدا کردن ریشه آن است. همین عملیات را برای پیدا کردن مقدار بهینه $$x$$ (در واقع $$R$$) به کار میبریم.
$$\large \dfrac {\partial \left( -x \ln(x) \right)}{\partial x} = -\ln(x) + \frac{1}{x}(-x) = -ln(x) -1 = 0 $$
در نتیجه خواهیم داشت:
$$ \large \ln(x) = -1 \rightarrow e^{-1} = x = \dfrac{1}{e} $$
در نتیجه به صورت تقریبی (با در نظر گرفتن حد و تبدیل جمع به انتگرال) نقطه بهینه برای مقدار $$R$$ برابر است با $$\dfrac{N}{e}$$ و بهترین کاندید با احتمال $$\frac{1}{e}$$ انتخاب میشود.
$$\large {\displaystyle P(x) = \dfrac{-1}{e} \ln(\dfrac{1}{e} ) = \dfrac{1}{e} \ln(e) = \dfrac{1}{e} \;} $$
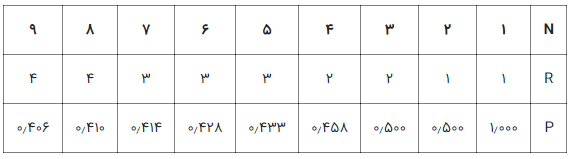
این محاسبات به ازاء بعضی از مقادیر $$N$$ و $$R$$ در جدول زیر دیده میشود.
این محاسبات را به کمک کد (شبه کد) زیر که به «زبان جولیا» (Julia) نوشته شده، انجام دادهایم.
1Ns = collect(1:50) # number of candidates
2P(R,N) = R/N*sum([1/(n-1) for n=R+1:N]) # define function P(R)
3Ropt = zeros(Int64,length(Ns)) # define vector for R*
4Popt = zeros(length(Ns)) # define vector for P(R*)
5for N in Ns # optimization loop
6 Popt[N], Ropt[N] = findmax([P(R,N) for R=1:N])
7endهمانطور که در جدول بالا مشاهده کردید، با داشتن استراتژی بهینه، اگر تعداد زیادی داوطلب در مسئله منشی و تصمیم بهینه وجود داشته باشد، احتمال انتخاب دقیقاً بهترین نامزد کاهش نمییابد. مقدار بهینه $$R^*$$ از یک رابطه خطی ساده با N پیروی میکند. از طرفی قانون مجانبی $$\dfrac{1}{e}$$ نیز به کمک ما میآید. این نسبت یا کسر، دقیقاً با مقداری احتمال موفقیت $$P(R)$$ برای $$N$$ بزرگ صدق میکند.
نکته: میدانید که $$e$$ نماد عدد اویلر است. نتیجه محاسبه $$\frac{1}{e}$$ نیز چیزی حدود 0٫37 خواهد شد که در نمودارهای زیر مشخص شده است.
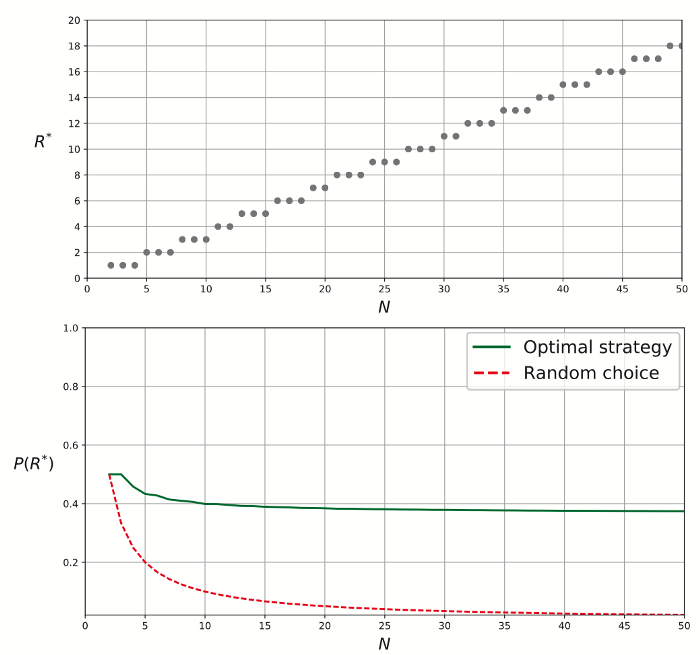
نمودار بالا به خوبی تفاوت بین «استراتژی بهینه» (Optimal Strategy) و «انتخاب تصادفی» (Random Choice) را نشان میدهد. با افزایش تعداد داوطلبها، همگرایی استراتژی بهینه در حدود احتمال ۰٫۳۷ مشخص است در حالیکه در حالت انتخاب تصادفی، احتمال پیدا کردن بهترین گزینه یا کاندید برای مسئله منشی و تصمیم بهینه نیز تقریبا صفر خواهد شد.
خلاصه و جمعبندی
در این نوشتار به یکی از مسائل جالب در حوزه بهینهسازی و احتمال به نام مسئله منشی و تصمیم بهینه پرداختیم. همانطور که دیدید، طرح یک مسئله بهینهسازی ریاضیاتی براساس احتمال شرطی ساخته و حل شد. جالب است که حاصل این بهینهسازی ما را به عکس عدد نپر ($$\frac{1}{e}$$) سوق میدهد. در این بین مثالهایی از طرحها و سناریوهای مختلف، برای روشنتر شدن موضوع نیز ارائه شد.










