مجموع ریمان — از صفر تا صد
در آموزشهای پیشین مجله فرادرس، درباره روشهای ذوزنقهای و سیمپسون برای حل انتگرال عددی بحث کردیم. در این آموزش، با روش مجموع ریمان (Riemann Sums) آشنا میشویم.
یک مجموع ریمان برای تابع $$ f ( x) $$ در بازه
$$ \large x _ 0 = a < x _ 1 < \cdots < x _ { N - 1 } < x _ N = b $$
مجموعی به فرم زیر است:
$$ \large \sum _ { i = 1 } ^ N f ( x _ i ^ * ) ( x _ i - x _ { i - 1 } ) \ \ , \ x _ i ^ * \in [ x _ { i - 1 } , x _ i ] $$
که در آن، هر مقدار $$ x_i^* \in [x_{i-1},x_i] $$ در هر زیربازه دلخواه است.
با استفاده از مجموع ریمان میتوان به سادگی مقدار یک انتگرال معین به فرم زیر را تقریب زد:
$$ \large \int _ a ^ b f ( x ) \, d x \approx \sum _ { i = 1 } ^ N f ( x _ i ^ * ) ( x _ i - x _ { i - 1 } ) \ \ , \ x _ i ^ * \in [ x _ { i - 1 } , x _ i ] $$
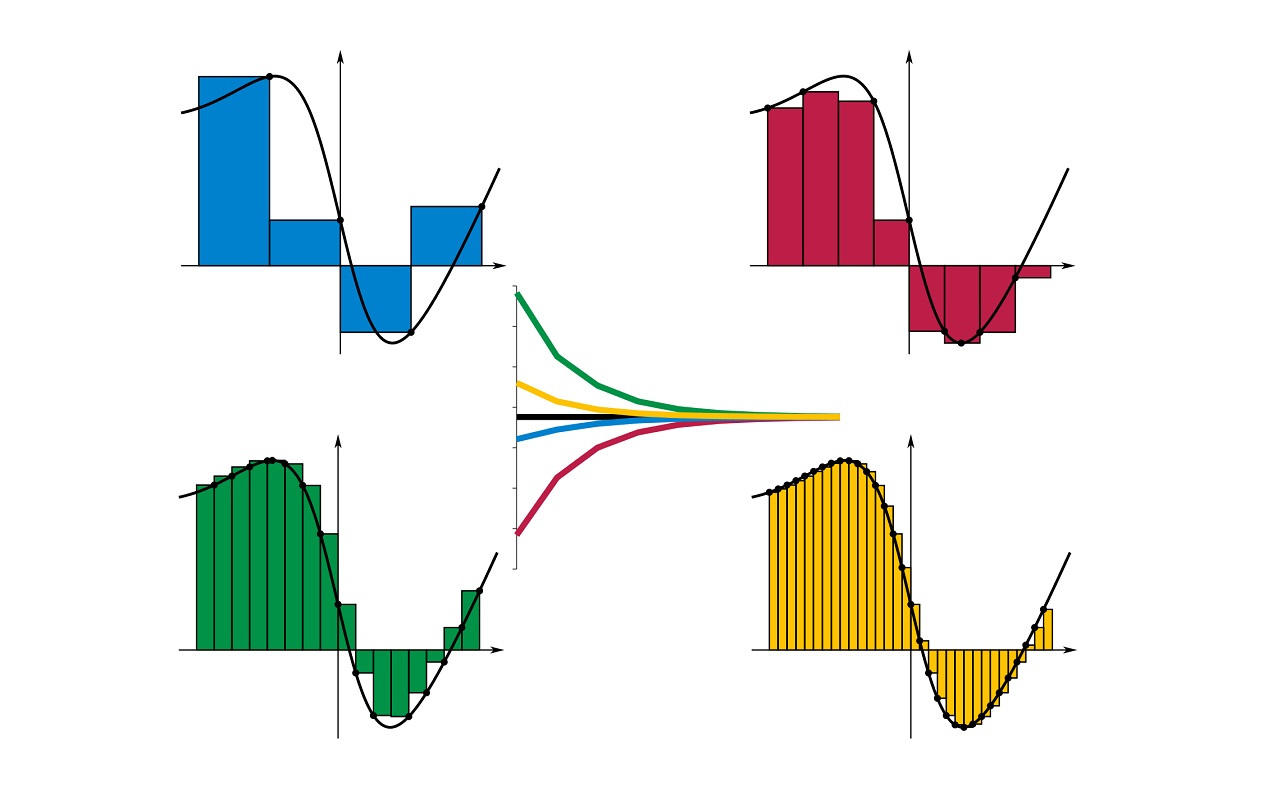
توجه کنید که ضرب $$ f(x_i^ * ) (x_i - x_{i-1}) $$ برای هر $$i$$، معرف مساحت یک مستطیل به طول $$ f(x_i^ * ) $$ و به عرض $$ x_i - x_{i-1} $$ است. میتوان یک مجموع ریمان را به عنوان مساحت $$N $$ مستطیل با طولهایی در نظر گرفت که با منحنی $$ y = f ( x) $$ تعیین میشوند.
مقدار $$ x_i^* $$ در هر زیربازه به صورت دلخواه انتخاب میشود. البته گزینههای خاصی نیز وجود دارند که میتوان از آنها استفاده کرد:
- مجموع ریمان چپ: اگر هر $$ x_i^* = x_{i-1} $$ نقطه انتهایی سمت چپ زیربازه $$ [x_{i-1},x_i] $$ باشد.
- مجموع ریمان راست: اگر هر $$x_i^* = x_i$$ نقطه انتهایی سمت راست زیربازه $$ [x_{i-1},x_i] $$ باشد.
- مجموع ریمان نقطه میانی: وقتی که هر $$ x_i^* = (x_{i-1} + x_i)/2 $$ نقطه میانی زیربازه $$ [x_{i-1},x_i] $$ باشد.
برای درک بهتر، مستطیلهای چپ، راست و نقطه میانی مجموع ریمان را برای تابع زیر مینویسیم:
$$ \large f ( x ) = \frac { 1 } { 1 + x ^ 2 } $$
بازه مورد نظر $$ [0, 5 ] $$ با تعداد زیربازه $$ N = 10 $$ است.
برنامه پایتون مربوط به رسم شکلهای این مستطیلها به صورت زیر است:
1f = lambda x : 1/(1+x**2)
2a = 0; b = 5; N = 10
3n = 10 # Use n*N+1 points to plot the function smoothly
4
5x = np.linspace(a,b,N+1)
6y = f(x)
7
8X = np.linspace(a,b,n*N+1)
9Y = f(X)
10
11plt.figure(figsize=(15,5))
12
13plt.subplot(1,3,1)
14plt.plot(X,Y,'b')
15x_left = x[:-1] # Left endpoints
16y_left = y[:-1]
17plt.plot(x_left,y_left,'b.',markersize=10)
18plt.bar(x_left,y_left,width=(b-a)/N,alpha=0.2,align='edge',edgecolor='b')
19plt.title('Left Riemann Sum, N = {}'.format(N))
20
21plt.subplot(1,3,2)
22plt.plot(X,Y,'b')
23x_mid = (x[:-1] + x[1:])/2 # Midpoints
24y_mid = f(x_mid)
25plt.plot(x_mid,y_mid,'b.',markersize=10)
26plt.bar(x_mid,y_mid,width=(b-a)/N,alpha=0.2,edgecolor='b')
27plt.title('Midpoint Riemann Sum, N = {}'.format(N))
28
29plt.subplot(1,3,3)
30plt.plot(X,Y,'b')
31x_right = x[1:] # Left endpoints
32y_right = y[1:]
33plt.plot(x_right,y_right,'b.',markersize=10)
34plt.bar(x_right,y_right,width=-(b-a)/N,alpha=0.2,align='edge',edgecolor='b')
35plt.title('Right Riemann Sum, N = {}'.format(N))
36
37plt.show()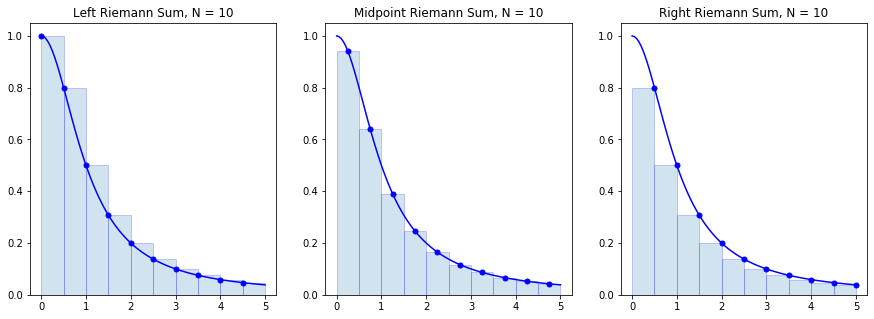
توجه کنید که وقتی تابع $$ f ( x ) $$ در بازه $$ [ a , b ] $$ نزولی باشد، نقطه انتهایی سمت چپ منجر به یک تقریب اضافی (موسوم به مجموع ریمان بالا) از انتگرال $$ \int_a^b f(x) dx $$ و نقاط انتهایی سمت راست منجر به یک تقریب نقصانی (معروف به مجموع ریمان پایین) خواهند شد. وقتی تابع صعودی باشد، عکس این مطلب برقرار است.
در اینجا، مقدار هر یک از مجموعهای ریمان را محاسبه میکنیم:
1dx = (b-a)/N
2x_left = np.linspace(a,b-dx,N)
3x_midpoint = np.linspace(dx/2,b - dx/2,N)
4x_right = np.linspace(dx,b,N)
5
6print("Partition with",N,"subintervals.")
7left_riemann_sum = np.sum(f(x_left) * dx)
8print("Left Riemann Sum:",left_riemann_sum)
9
10midpoint_riemann_sum = np.sum(f(x_midpoint) * dx)
11print("Midpoint Riemann Sum:",midpoint_riemann_sum)
12
13right_riemann_sum = np.sum(f(x_right) * dx)
14print("Right Riemann Sum:",right_riemann_sum)پاسخ حاصل از اجرای این برنامه به صورت زیر است:
Partition with 10 subintervals. Left Riemann Sum: 1.613488696614725 Midpoint Riemann Sum: 1.373543428316664 Right Riemann Sum: 1.1327194658454942
مقدار دقیق انتگرال را میدانیم:
$$ \large \int _ 0 ^ 5 \frac { 1 } { 1 + x ^ 2 } d x = \arctan ( 5 ) $$
و میتوانیم مجموع ریمان را با حاصل این انتگرال مقایسه کنیم.
مقدار دقیق انتگرال به صورت زیر در پایتون محاسبه میشود:
1I = np.arctan(5)
2print(I)1.373400766945016
مقایسه مقدار دقیق با مقادیر تقریبی نیز به صورت زیر انجام میشود:
1print("Left Riemann Sum Error:",np.abs(left_riemann_sum - I))
2print("Midpoint Riemann Sum:",np.abs(midpoint_riemann_sum - I))
3print("Right Riemann Sum:",np.abs(right_riemann_sum - I))نتیجه این مقایسه به صورت زیر است:
Left Riemann Sum Error: 0.24008792966970915 Midpoint Riemann Sum: 0.00014266137164820059 Right Riemann Sum: 0.24068130109952168
فرمولهای خطای مجموع ریمان
مجموع ریمان تقریبی از انتگرال معین است. پرسشی که در این اینجا پیش میآید این است که یک مجموع ریمان تا چه اندازه تقریب مناسبی است؟ قضیه زیر پاسخ این پرسش است.
قضیه ۱: فرض کنید $$ L_N(f) $$ مجموع ریمان چپ را نشان میدهد:
$$ \large L _ N ( f ) = \sum _ { i = 1 } ^ N f ( x _ { i - 1 } ) \Delta x $$
که در آن، $$ \Delta x = (b-a)/N $$ و $$ x_i = a + i \Delta x $$. محدوده خطا به صورت زیر خواهد بود:
$$ \large E _ N ^ { L } ( f ) = \left | \ \int _ a ^ b f ( x ) \ d x - L _ N ( f ) \ \right | \leq \frac { ( b - a ) ^ 2 } { 2 N } K _ 1 $$
که در آن برای هر $$ x \in [a,b] $$ رابطه $$ \left| \, f'(x) \, \right| \leq K_1 $$ برقرار است.
قضیه ۲: فرض کنید $$ R_N(f)$$ مجموع ریمان راست زیر باشد:
$$ \large R _ N ( f ) = \sum _ { i = 1 } ^ N f ( x _ { i } ) \Delta x $$
که در آن، $$ \Delta x = (b-a)/N $$ و $$ x_i = a + i \Delta x $$. کران خطا به صورت زیر است:
$$ \large E _ N ^ { R } ( f ) = \left | \ \int _ a ^ b f ( x ) \ d x - R _ N ( f ) \ \right | \leq \frac { ( b - a ) ^ 2 } { 2 N } K _ 1 $$
که در آن، برای هر $$ x \in [a,b] $$، رابطه $$ \left| \, f'(x) \, \right| \leq K_1 $$ برقرار است.
قضیه ۳: مجموع ریمان نقطه میانی $$ M_N(f) $$ زیر را در نظر بگیرید:
$$ \large M _ N ( f ) = \sum _ { i = 1 } ^ N f ( x _ i ^ * ) \Delta x $$
که در آن، برای $$ x_i = a + i \Delta x $$، روابط $$ \Delta x = (b-a)/N $$ و $$ x_i^* = (x_{i-1} + x_i)/2 $$ را داریم. کران خطا به صورت زیر است:
$$ \large E _ N ^ { M } ( f ) = \left | \ \int _ a ^ b f ( x ) \ d x - M _ N ( f ) \ \right | \leq \frac { ( b - a ) ^ 3 } { 2 4 N ^ 2 } K _ 2 $$
که در آن، برای هر $$ x \in [a,b] $$، رابطه $$ \left| \, f^{\prime \prime}(x) \, \right| \leq K_2 $$ برقرار است.
ذکر چند نکته زیر ضروری است:
- مجموعهای ریمان چپ و راست کران خطای مشابهی دارند که به مشتق اول $$ f'(x) $$ بستگی دارند.
- خطای مجموع ریمان نقطه میانی به مشتق دوم $$ f^{\prime \prime}(x) $$ وابسته است.
- انتظار میرود مجموع ریمان نقطه میانی وقتی $$ N \to \infty$$، تقریب بهتری داشته باشد، زیرا کران خطای آن تناسب عکس با $$ N ^2 $$ دارد، اما کران خطای مجموعهای چپ/راست ریمان تنها با $$ N $$ رابطه عکس دارد.
پیادهسازی مجموع ریمان در پایتون
برای پیادهسازی مجموع ریمان، تابع riemann_sum را مینویسیم که پنج ورودی f و a و b و N و method دارد و خروجی آن، مجموع ریمان زیر است:
$$ \large \sum _ { i = 1 } ^ N f ( x _ i ^ * ) \Delta x $$
که در آن، $$ \Delta x = (b-a)/N $$ و $$ x_i = a + i\Delta x $$ افرازی با $$N$$ زیربازه به طول مساوی را نشان میدهد. همچنین، method مشخص میکند که یکی از نقاط انتهایی چپ (مجموع ریمان چپ)، نقاط انتهایی راست (مجموع ریمان راست) یا نقاط میانی (مجموع ریمان نقطه میانی) استفاده شود. روش پیشفرض نقطه میانی است.
1def riemann_sum(f,a,b,N,method='midpoint'):
2 '''Compute the Riemann sum of f(x) over the interval [a,b].
3
4 Parameters
5 ----------
6 f : function
7 Vectorized function of one variable
8 a , b : numbers
9 Endpoints of the interval [a,b]
10 N : integer
11 Number of subintervals of equal length in the partition of [a,b]
12 method : string
13 Determines the kind of Riemann sum:
14 right : Riemann sum using right endpoints
15 left : Riemann sum using left endpoints
16 midpoint (default) : Riemann sum using midpoints
17
18 Returns
19 -------
20 float
21 Approximation of the integral given by the Riemann sum.
22 '''
23 dx = (b - a)/N
24 x = np.linspace(a,b,N+1)
25
26 if method == 'left':
27 x_left = x[:-1]
28 return np.sum(f(x_left)*dx)
29 elif method == 'right':
30 x_right = x[1:]
31 return np.sum(f(x_right)*dx)
32 elif method == 'midpoint':
33 x_mid = (x[:-1] + x[1:])/2
34 return np.sum(f(x_mid)*dx)
35 else:
36 raise ValueError("Method must be 'left', 'right' or 'midpoint'.")حال صحت عملکرد این برنامه را آزمایش میکنیم. برای مثال، تابع زیر را در نظر بگیرید:
$$ \large \int_0^{\pi/2} \sin(x) \, dx = 1 $$
از آنجایی که $$\sin(x)$$ در بازه $$ [0,\pi/2]$$ صعودی است، میدانیم نقاط انتهایی سمت چپ یک تقریب نقصانی و نقاط انتهایی راست، یک تقریب اضافی خواهند داشت.
برنامهها و جوابهای زیر این موضوع را نشان میدهند:
1riemann_sum(np.sin,0,np.pi/2,100)1.0000102809119054
1riemann_sum(np.sin,0,np.pi/2,100,'right')1.007833419873582
1riemann_sum(np.sin,0,np.pi/2,100,'left')0.992125456605633
همچنین، میدانیم که $$ \int_0^1 x \, dx = 1/2$$ و نقطه میانی باید نتیجهای دقیق برای $$N$$ داشته باشد:
1riemann_sum(lambda x : x,0,1,1)0.5
مثالها
در این بخش چند مثال را بیان میکنیم.
مثال ۱
مقدار $$ N $$ را به گونهای تعیین کنید که تضمین شود مجموع انتگرال راست $$ f(x)=\frac{4}{1 + x^2}$$ روی بازه $$ [0,1]$$ به اندازه $$ 10 ^{-5}$$ با مقدار دقیق زیر اختلاف داشته باشد:
$$ \large \int _ 0 ^ 1 \frac { 4 } { 1 + x ^ 2 } d x = \pi $$
حل: ابتدا مشتق انتگرالده را به صورت زیر محاسبه میکنیم:
$$ \large f' ( x ) = - \frac { 8 x } { ( 1 + x ^ 2 ) ^ 2 } $$
برای پیدا کردن یک کران $$ \left| f'(x) \right| $$ روی $$ [ 0 , 1 ] $$ از بهینهسازی جستوجوی جامع (Brute-force Search) استفاده میکنیم:
1x = np.linspace(0,1,1000)
2y = np.abs(-8*x/(1 + x**2)**2)
3np.max(y)2.5980759093919907
بنابراین، برای هر $$ x \in [0,1] $$، رابطه $$ \left| f'(x) \right| \leq 2.6 $$ را خواهیم داشت. از کران خطای زیر استفاده میکنیم:
$$ \large \frac { ( b - a ) ^ 2 } { 2 N } K _ 1 \leq 1 0 ^ { - 5 } \ \Rightarrow \ \frac { 1 . 3 } { N } \leq 1 0 ^ { - 5 } \ \Rightarrow \ 1 3 0 0 0 0 \leq N $$
مجموع ریمان راست را برای $$ N=130000 $$ محاسبه میکنیم:
1approximation = riemann_sum(lambda x : 4/(1 + x**2),0,1,130000,method='right')
2print(approximation)3.1415849612722386
اکنون دقت تقریب را اعتبارسنجی میکنیم:
1np.abs(approximation - np.pi) < 10**(-5)که جواب آن به صورت زیر است:
True
مثال ۲
مقدار $$N$$ را طوری به دست آورید که تضمین کند مجموع ریمان نقطه میانی $$ f(x)=\frac{1}{x} $$ روی $$ [1 , 2 ] $$ برای انتگرال دقیق زیر $$ 10 ^ { - 8 } $$ باشد:
$$ \large \int_1^2 \frac{1}{x} dx = \ln(2) $$
حل: مشتق دوم زیر را محاسبه میکنیم:
$$ \large f^{\prime\prime}(x) = \frac{2}{x^3} $$
از آنجایی که $$ f ^ { \prime \prime } $$ برای هر $$ x > 0 $$ نزولی است، برای هر $$ x \in [1,2]$$، نامساوی $$\left| \, f^{\prime \prime}(x) \, \right| \leq 2 $$ را داریم. از کران خطای زیر استفاده میکنیم:
$$ \large \frac { ( b - a ) ^ 3 } { 2 4 N ^ 2 } K _ 2 \leq 1 0 ^ { - 8 } \ \Rightarrow \ \frac { 1 } { 1 2 N ^ 2 } \leq 1 0 ^ { - 8 } \Rightarrow \frac { 1 0 ^ 4 } { \sqrt { 1 2 } } \leq N $$
110**4 / np.sqrt(12)2886.751345948129
بنابراین، یک افراز به تعداد $$ N=2887 $$ دقت مورد نظر را تضمین میکند:
1approximation = riemann_sum(lambda x : 1/x,1,2,2887,method='midpoint')
2print(approximation)0.6931471768105913
حال، دقت این تقریب را به صورت زیر اعتبارسنجی میکنیم:
1np.abs(approximation - np.log(2)) < 10**(-8)True
مثال ۳
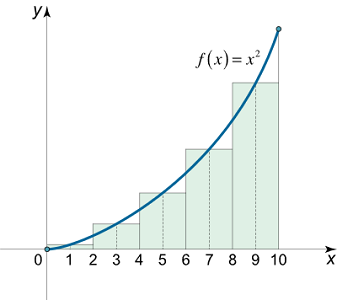
مساحت زیر منحنی $$ f\left( x \right) = {x^2} $$ را روی بازه $$[0,10]$$ با استفاده از مجموع ریمان میانی برای $$ n = 5 $$ به دست آورید.
حل: بازه $$[0,10] $$ را به ۵ زیربازه مساوی با نقاط میانی زیر تبدیل میکنیم:
$$ \large { { x _ i } = \left \{ { 0 , 2 , 4 , 6 , 8 , 1 0 } \right \} . } $$
نقاط میانی $${\xi _i} $$ زیربازهها دارای مختصات زیر هستند:
$$ \large { { \xi _ i } = \left \{ { 1 , 3 , 5 , 7 , 9 } \right \} . } $$
بنابراین، مجموع ریمان نقطه میانی به صورت زیر خواهد بود:
$$ \large { M _ 5 } = \sum \limits _ { i = 1 } ^ 5 { f \left ( { { \xi _ i } } \right ) \Delta x } $$
که در آن، $$\Delta x = 2$$ طول هر زیربازه است.
با محاسبه مقادیر $$ {f\left( {{\xi _i}} \right)}$$، مقدار تقریبی مساحت به صورت زیر به دست میآید:
$$ \large \begin {align*}
{ A \approx { M _ 5 } } & = { \sum \limits _ { i = 1 } ^ 5 { f \left ( { { \xi _ i } } \right ) \Delta x } } = { \Delta x \sum \limits _ { i = 1 } ^ 5 { f \left ( { { \xi _ i } } \right ) } } \\ & = { \Delta x \left [ { f \left ( { { \xi _ 1 } } \right ) + f \left ( { { \xi _ 2 } } \right ) + \cdots + f \left ( { { \xi _ 5 } } \right ) } \right ] } \\ & = { 2 \left ( { { 1 ^ 2 } + { 3 ^ 2 } + { 5 ^ 2 } + { 7 ^ 2 } + { 9 ^ 2 } } \right ) } \\ & = { 2 \left ( { 1 + 9 + 25 + 49 + 81 } \right ) } = { 3 3 0 . }
\end {align*} $$
مثال ۴
مساحت زیر منحنی $$y = 1 – {x^2} $$ را در بازه $$[0,1]$$ با استفاده از مجموع ریمان چپ برای $$n$$ زیربازه و با حد $$ n \to \infty $$ محاسبه کنید.
حل: با فرض اینکه بازه $$[0,1]$$ را به $$n$$ زیربازه مساوی تقسیم کنیم، اندازه هر زیربازه برابر است با:
$$ \large \Delta x = \frac { 1 } { n } . $$
مختصات نقاط افراز به صورت زیر محاسبه میشود:
$$ \large { { x _ i } = a + i \Delta x } = { 0 + i \cdot \frac { 1 } { n } } = { \frac { i } { n } } $$
در مجموع ریمان راست، نقاط اختیاری $${\xi _i}$$ به گونهای انتخاب میشوند که
$$\large {\xi _i} = {x_i} = \frac{i}{n}. $$
بنابراین، داریم:
$$ \large { f \left ( { { \xi _ i } } \right ) } = { f \left ( { { x _ i } } \right ) } = { 1 – x _ i ^ 2 } = { 1 – { \left ( { \frac { i } { n } } \right ) ^ 2 } } = { \frac { { { n ^ 2 } – { i ^ 2 } } }{ { { n ^ 2 } } } } $$
مجموعهای اخیر به صورت زیر محاسبه میشوند:
$$ \large { \sum \limits _ { i = 1 } ^ n { { n ^ 2 } } } = { { n ^ 2 } \sum \limits _ { i = 1 } ^ n 1 } = { { n ^ 2 } \cdot n } = { { n ^ 3 } ; } \\ \large { \sum \limits _ { i = 1 } ^ n { { i ^ 2 } } } = { \frac { { n \left ( { n + 1 } \right ) \left ( { 2 n + 1 } \right ) } } { 6 } } = { \frac { { 2 { n ^ 3 } + 3 { n ^ 2 } + n } } { 6 } . } $$
بنابراین، خواهیم داشت:
$$ \large \begin {align*} { { R _ n } } & = { \frac { 1 } { { { n ^ 3 } } } \left ( { \sum \limits _ { i = 1 } ^ n { { n ^ 2 } } – \sum \limits _ { i = 1 } ^ n { { i ^ 2 } } } \right ) } = { \frac { 1 } { { { n ^ 3 } } } \left ( { { n ^ 3 } – \frac { { 2 { n ^ 3 } + 3 { n ^ 2 } + n } } { 6 } } \right ) } \\ & = { \frac { 1 } { { { n ^ 3 } } } \cdot \frac { { 4 { n ^ 3 } – 3 { n ^ 2 } – n } }{ 6 } } = { \frac { { 4 { n ^ 2 } – 3 n – 1 } } { { 6 { n ^ 2 } } } . } \end {align*} $$
اکنون مساحت ناحیه زیر منحنی را با حد $$n \to \infty $$ مجموع ریمان محاسبه میکنیم:
$$ \large \begin {align*}
A & = \lim \limits _ { n \to \infty } { R _ n } = { \lim \limits _ { n \to \infty } \frac { { 4 { n ^ 2 } – 3 n – 1 } } { { 6 { n ^ 2 } } } } \\ & = { \lim \limits _ { n \to \infty } \frac { { 4 – \frac { 3 } { n } – \frac { 1 } { { { n ^ 2 } } } } } { 6 } } = { \frac { 4 } { 6 } } = { \frac { 2 } { 3 } . }
\end {align*} $$
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش محاسبات عددی با MATLAB
- مجموعه آموزشهای محاسبات عددی
- آموزش ریاضی پایه دانشگاهی
- انتگرال ریمان استیلتیس (Riemann Stieltjes) — مفاهیم و کاربردها
- دستگاه معادلات خطی — به زبان ساده
- جذر یا محاسبه ریشه دوم عدد — به زبان ساده
^^










