مثلث چیست؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)

مثلثها اشکالی سهضلعی و دارای سه زاویه هستند که با اتصال هر سه نقطه در صفحه میتوان آنها را شکل داد. مثلث یکی از اولین شکلهایی است که در هندسه مطالعه میشود. در این آموزش یه این پرسش پاسخ میدهیم که مثلث چیست و علاوه بر آن، با ویژگیهای مثلث و انواع آن آشنا میشویم.
فیلم آموزشی مثلث
مثلث چیست ؟
مثلث یکی از اشکال هندسی است که از اهمیت ویژهای برخوردار است، زیرا چندضلعیهای دیگر (با تعداد ضلعهای 4، 5، 6 یا n ضلع دلخواه) را میتوان به مثلث تجزیه کرد. بنابراین، درک ویژگیهای اساسی مثلثها امکان مطالعه عمیق چندضلعیهای بزرگتر را نیز فراهم میکند.
جالب این است که مثلث تنها چندضلعی است که اگر طول اضلاع آن داده شود، یک مثلث منحصر به فرد را میسازد. به همین دلیل، با داشتن برخی اطلاعات در مورد یک مثلث (به عنوان مثال طول برخی از ضلعها و برخی زاویهها)، امکان تعیین اطلاعات اضافه در مورد مثلثها وجود دارد.
وقتی با مثلثها سر و کار داریم، اصطلاحاتی را به کار میبریم که باید مفهوم آنها را بدانیم. در ادامه، با این موارد آشنا میشویم.
- ضلع: پارهخطی است که دو رأس مجاور مثلث را به هم پیوند میدهد.
- رأس: محل برخورد دو ضلع مثلث را رأس میگویند.
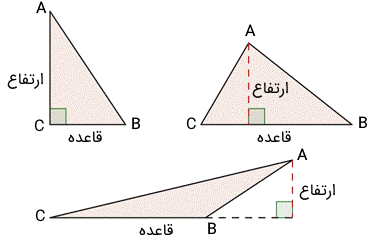
- ارتفاع: پارهخطی است که از یک رأس آغاز میشود و بر ضلع مقابل (یا امتداد آن) عمود است. محل برخورد ارتفاع با قاعده یا امتداد آن، پای عمود نام دارد.
- قاعده: ضلعی را که ارتفاع بر آن عمود است قاعده مثلث نام دارد.
مجموع زوایای یک مثلث
اگر $$ABC$$ یک مثلث باشد، آنگاه $$ \angle ABC + \angle BCA + \angle CAB = 180^\circ $$. به عبارت دیگر، مجموع زوایای یک مثلث برابر با $$180^ \circ $$ است.
اثبات: برای اثبات گفته بالا، شکل زیر را در نظر بگیرید.
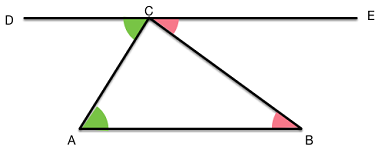
خط $$DE$$ را موازی با $$AB$$ رسم میکنیم و مانند شکل بالا از $$C$$ عبور میدهیم. از آنجا که $$AB$$ موازی $$DE$$ است ($$ DE \parallel AB $$)، میتوانیم با استفاده از قاعده زوایای متبادل داخلی به $$\angle DCA = \angle CAB$$ و $$\angle BCE = \angle CBA$$ برسیم. از آنجا که مجموع زاویههای یک خط 180 درجه است، تساوی $$ \angle DCA + \angle ACB + \angle BCE = 180^ \circ $$ را خواهیم داشت.
بنابراین، نتیجه خواهیم گرفت:
$$ \large \angle CAB + \angle ACB + \angle CBA = \angle DCA + \angle ACB + \angle BCE = 180^ \circ $$
زاویههای خارجی مثلث
اندازه زاویه خارجی یک مثلث برابر با مجموع دو زاویه داخلی غیرمجاور آن است. زاویههای داخلی غیرمجاور، زاویههای داخلی یک مثلث هستند که مخالف زاویه خارجی مورد بررسی هستند.
اثبات: در مثلث زیر باید ثابت کنیم:
$$\large \angle ABC+\angle CAB=\angle DCA .$$
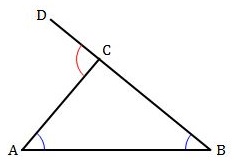
میدانیم که مجموع زاوایای یک مثلث 180 است. بنابراین، در مثلث $$ABC$$ تساوی $$ \angle ABC + \angle BCA + \angle CAB = 180^\circ $$ را داریم.
از آنجا که $$\angle BCA$$ و $$\angle DCA$$ یک خط مستقیم را تشکیل میدهند، مجموع زاویه آنها برابر با ۱۸۰ درجه است. بنابرین، دو مجموعه زاویه داریم که برابر با ۱۸۰ درجه هستند. با برابر قرار دادن آنها با یکدیگر، داریم:
$$ \large \angle ABC + \angle BCA + \angle CAB = \angle BCA + \angle DCA. $$
بنابراین، تساوی به راحتی اثبات میشود:
$$ \large \angle ABC + \angle CAB = \angle DCA. $$
نامساوی مثلثی
مثلثها خاصیتی دارند که مجموع هر دو ضلع مثلث همیشه بزرگتر از ضلع سوم است. این ویژگی به نامساوی مثلثی معروف است.
شکل زیر سه مثلث مختلف را نشان میدهد که برای همه آنها نامساوی مثلثی برقرار است.
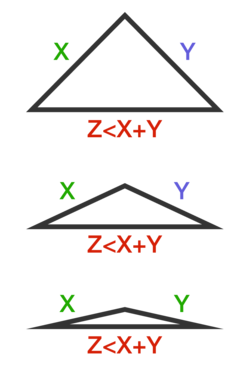
نامساوی مثلثی از این موضوع نتیجه شده که کوتاهترین مسیر بین دو نقطه خط مستقیمِ متصلکننده آن دو نقطه است. مثلاً اگر اندازه دو ضلع از یک مثلث برابر با ۶ و ۵ باشد، آنگاه اندازه ضلع سوم قطعاً کمتر از ۱۱ خواهد بود.
انواع مثلث بر اساس اضلاع
هنگام مقایسه طول اضلاع مثلث، هر سه ضلع ممکن است برابر باشد، دو ضلع از آنها مساوی باشند یا هر سه ضلع طولهای متفاوتی داشته باشند. این موارد اساس دستهبندی مثلثها را تشکیل میدهد.
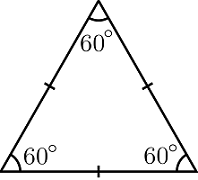
مثلث متساوی الاضلاع
در یک مثلث متساوی الاضلاع طول همه ضلعها برابر است. «متساوی الاضلاع» از دو کلمه گرفته شده است: «متساوی» به معنی «برابر» و «الاضلاع» هم مشخصاً به معنی «اضلاع» است. از آنجا که اضلاع مساوی در یک مثلث زاویه برابر میسازند، تمام زاویههای یک مثلث متساوی برابر هستند و همچنین، اندازه هریک برابر با 60 درجه است.
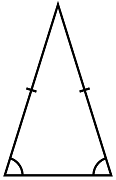
مثلث متساوی الساقین
مثلث متساوی الساقین دو ضلع برابر (و در نتیجه دو زاویه مساوی) دارد. دو ضلع برابر در مقابل دو زاویه مساوی هستند. از آنجا که هر دو ضلع مثلث متساوی الساقین برابر هستند، همه مثلثهای متساوی الاضلاع مثلث متساوی الساقین نیز هستند، اما مثلثهای متساوی الساقین الزاماً متساوی الاضلاع نیستند.
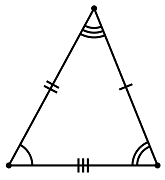
مثلث مختلف الاضلاع
در یک مثلث مختلف الاضلاع، تمام اضلاع دارای طولهای متفاوتی هستند. اگر یک مثلث متساوی الاضلاع نباشد، یک مثلث مختلف الاضلاع است.
مثلث تباهیده
به مثلثی تباهیده گفته میشود که تمام رئوس آن همخط باشند، بنابراین طول دو ضلع مثلث به طول ضلع سوم اضافه میشود. چنین مثلثی شبیه یک مثلث به نظر نمیرسد بیشتر شبیه یک پارهخط است.
انواع مثلث بر اساس زاویه
اگر بخواهیم مثلثها را بر اساس زاویه تقسیمبندی کنیم، میتوانیم سه دسته زیر را نام ببریم:
- مثلث حاده: وقتی زاویه بین هر دو ضلع مثلث کمتر از 90 درجه باشد، آن را مثلث حاده مینامند.
- مثلث قائم الزاویه: وقتی زاویه بین یک جفت ضلع مثلث برابر 90 درجه باشد، آن را مثلث قائم الزاویه مینامند.
- مثلث منفرجه: وقتی زاویه بین یک جفت ضلع مثلث بیشتر از 90 درجه باشد، آن را مثلث منفرجه مینامند.
- مثلث متساوی الزاویه: اگر در مثلثی، هر سه زاویه 60 درجه باشند، به آن متساوی الزاویه میگوییم. چنین مثلثی مثلث متساوی الاضلاع نیز هست.

مساحت مثلث
مساحت مثلث را میتوان با روشهای مختلفی محاسبه کرد که در ادامه آنها را معرفی میکنیم. برای آشنایی بیشتر با روشهای محاسبه مساحت مثلث، پیشنهاد میکنیم آموزش «مساحت مثلث — به زبان ساده (+ فیلم آموزش رایگان)» را مطالعه کنید.
مساحت مثلث با قاعده و ارتفاع
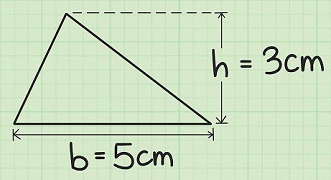
برای محاسبه مساحت یک مثلث باید طول قاعده و ارتفاع آن را داشته باشیم. با دانستن این دو مقدار و استفاده از فرمول زیر میتوانیم به مساحت یک مثلث پی ببریم:
$$ \large A = \frac 12 b h $$
رابطه بالا بیان میکند که مساحت یک مثلث، برابر با نصف حاصل ضرب اندازه قاعده (b) در ارتفاع (h) است. توجه کنید که هر کدام از ضلعهای مثلث را میتوان به عنوان قاعده در نظر گرفت، در این صورت در محاسبه ارتفاع باید دقت لازم را داشته باشیم.
مثلاً برای محاسبه مساحت مثلثی که در شکل بالا آمده است، داریم:
$$ \large A = \frac 12 b h = \frac 12 (5)(3) = 7.5 \; \text{cm}^2 $$
مساحت مثلث با سه ضلع
طبق فرمول هرون، مساحت یک مثلث با اضلاعی به طول $$a$$، $$b$$ و $$c$$ را میتوان با رابطه زیر محاسبه کرد:
$$ \large A= \sqrt{s(s-a)(s-b)(s-c)} $$
که در آن، $$s$$ برابر با نصف محیط (مجموع طول سه ضلع) مثلث است:
$$ \large s = \frac {a+b+c} { 2 } $$
محیط مثلث
در این بخش، روش محاسبه محیط مثلث را بیان میکنیم. برای آشنایی بیشتر با روشهای محاسبه محیط مثلث، پیشنهاد میکنیم آموزش «محیط مثلث — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» را مطالعه کنید.
محیط مثلث با داشتن سه ضلع
سادهترین روش برای محاسبه محیط یک مثلث، جمع کردن طول اضلاع آن با یکدیگر است؛ البته این در صورتی است که طول همه ضلعهای آن را بدانیم.
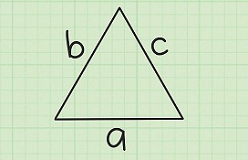
محیط مساحت شکل بالا برابر است با:
$$ \large P = a + b +b c $$
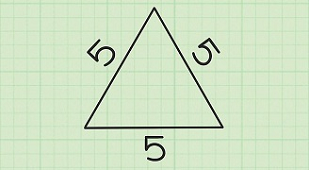
مثلاً مثلث شکل زیر را در نظر بگیرید. طول هر ضلع این مثلث 5 سانتیمتر است. پس این مثلث متساوی الاضلاع بوده و محیط آن 15 سانتیمتر است.
در محاسبه محیط مثلث دقت کنید که اگر ضلعهای آن بر حسب واحدهای مختلفی نوشته شده باشد، برای محاسبه محیط باید همه ضلعها را به یک واحد یکسان تبدیل کنید. مثلاً اگر دو ضلع برحسب سانتیمتر و یک ضلع برحسب میلیمتر داده شده باشد، ضلع میلیمتر را (با تقسیم بر ۱۰) به سانتیمتر تبدیل کرده و سپس با یکدیگر جمع کنید.
محیط مثلث با داشتن دو ضلع
اگر یکی از اضلاع مثلث مشخص نباشد، با دو روش میتوانیم ضلع سوم را پیدا کنیم و محیط را به دست آوریم.
اگر مثلث قائم الزاویه باشد، از قانون فیثاغورس استفاده میکنیم. قانون فیثاغورس بیان میکند که مربع (توان دو) وتر (ضلع بزرگتر) با مجموع مربعهای دو ضلع دیگر برابر است.
مثلاً فرض کنید که میخواهیم محیط مثلث شکل زیر را محاسبه کنیم. همانگونه که میبینیم، اندازه یک ضلع را نداریم و برای محاسبه آن باید از قضیه فیثاغورس استفاده کنیم.
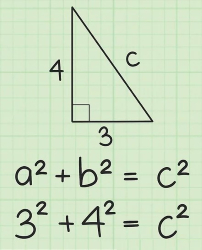
از محاسبات بالا، $$C = 5 $$ به دست میآید. اکنون که هر سه ضلع مثلث را داریم، با جمع آنها محیط مثلث را حساب میکنیم:
$$ \large P = 3 + 4 + 5 = 12 $$
اما اگر مثلث قائم الزاویه نباشد، میتوانیم از قانون کسینوسها برای یافتن ضلع مجهول استفاده کنیم. این قانون به صورت زیر است:
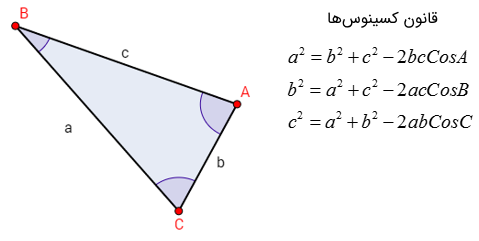
توجه کنید که رابطه فیثاغورس حالت خاصی از قانون کسینوسها است. قانون کسینوسها را میتوان برای هر سه زاویه داخلی معتبر است.
مثال های مثلث
در این بخش مثالهای متنوعی را درباره مثلث حل میکنیم.
مثال اول مثلث
اگر مثلثی دارای زاویههایی به اندازههای 50، 60 و 70 درجه باشد، نوع آن را تعیین کنید.
حل: هر سه زاویه متفاوت هستند، بنابراین طول همه اضلاع متفاوت است. از این رو، این یک مثلث مختلف الاضلاع داریم.
مثال دوم مثلث
مثلثی را با طول اضلاع 2، 3 و 6 واحد در چه دستهای از مثلثها قرار میگیرد؟
حل: این اعداد همه متفاوت هستند و به نظر میرسد نشاندهنده یک مثلث مختلف الاضلاع باشد. با این حال، با توجه به نابرابری مثلثی، چنین مثلثی نمیتواند وجود داشته باشد. زیرا مجموع هر دو ضلع مثلث همیشه بزرگتر از ضلع سوم است.
مثال سوم مثلث
مثلث زیر از چه نوعی است؟
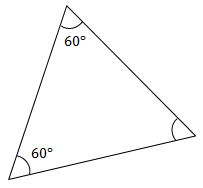
حل: از آنجا که مجموع سه زاویه در یک مثلث برابر با ۱۸۰ درجه است، زاویه مجهول مثلث بالا برابر خواهد بود با:
$$\large 180^\circ-60^\circ-60^\circ=60^\circ$$
بنابراین، هر سه زاویه برابر 60 درجه و مثلث متساوی الاضلاع است.
مثال چهارم مثلث
مثلث زیر از چه نوعی است؟
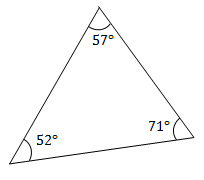
حل: هر سه زاویه در مثلث بالا زاویههای حاده، یعنی کوچکتر از 90 درجه هستند. از این رو، طبق تعریف، مثلث حاده است.
مثال پنجم مثلث
مثلث زیر از چه نوعی است؟
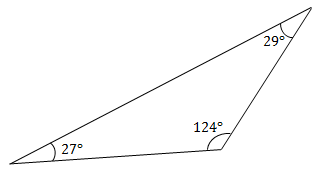
حل: زاویه 124 درجه در مثلث بالا منفرجه، یعنی بزرگتر از 90 درجه است. از این رو، طبق تعریف، مثلث منفرجه است.
مثال ششم مثلث
کدامیک از مثلثهای زیر متساوی الساقین است؟

حل: از آنجا که مجموع سه زاویه هر مثلث همیشه برابر با 180 درجه است، می توان مقدار زاویه نشان داده نشده را برای هر مثلث محاسبه کرد. این زاویهها برای مثلثهای $$A$$، $$B$$، $$C$$ و $$D$$ به صورت زیر محاسبه میشوند:
$$ \large \begin {aligned} 180 ^ \circ - 1 0 4 ^ \circ - 3 8 ^ \circ & = 3 8 ^ \circ & ( A ) \\ 180 ^ \circ - 90 ^ \circ - 55 ^ \circ & = 3 5 ^ \circ & ( B ) \\ 180 ^ \circ - 146 ^ \circ - 12 ^ \circ & = 22 ^ \circ & (C)\\ 180 ^ \circ-61^\circ-52^\circ&=67^\circ. & (D) \end{aligned} $$
فقط مثلث $$A$$ دارای دو زاویه مساوی است و بنابراین جواب مثلث $$A$$ است. مشاهده میکنید که مثلث $$B$$ یک مثلث قائم الزاویه، مثلث $$C$$ یک مثلث منفرجه و مثلث $$D$$ یک مثلث حاده است.
مثال هفتم مثلث
نسبت سه زاویهای که یک مثلث را تشکیل میدهند $$1:2:3$$ است. نوع این مثلث را تعیین کنید.
حل: از آنجا که مجموع سه زاویه 180 درجه است، مقادیر مربوط به سه زاویه برابر است با:
$$ \large \begin {aligned} 180 ^ \circ \times \frac { 1 }{ 6 } & = 3 0 ^ \circ \\ 180 ^ \circ \times \frac { 2 } { 6 } & = 6 0 ^ \circ \\ 180 ^ \circ \times \frac { 3 } { 6 } & = 9 0 ^ \circ . \end {aligned} $$
یکی از زاویهها زاویه قائمه است، بنابراین این مثلث قائم الزاویه است.
مثال هشتم مثلث
در شکل زیر، خطوط $$l_1$$ و $$l_2$$ موازی هستند. اگر $$ \angle BAD=75^\circ $$ و $$ \angle ACE=150^\circ $$، نوع $$ \triangle ABC $$ را تعیین کنید.
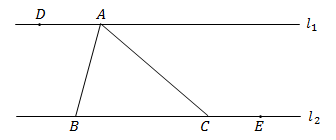
حل: از آنجا که دو خط $$l_1$$ و $$l_2$$ موازی هستند، داریم:
$$ \large \angle BAD=\angle ABC=75^\circ . $$
همچنین، با توجه به $$ \angle ACB=180^\circ-\angle ACE=180^\circ-150^\circ=30^\circ $$، خواهیم داشت:
$$ \large \angle BAC = 180 ^ \circ - \angle ACB - \angle ABC = 180 ^ \circ - 75 ^ \circ - 30 ^ \circ = 7 5 ^ \circ . $$
بنابراین، $$\angle BAC=\angle ABC=75^\circ $$ که نتیجه میدهد $$ \triangle ABC $$ متساوی الساقین است.
مثال نهم مثلث
مساحت مثلث زیر برابر با $$24\; \text{cm}^2$$ است. اگر $$a=6\, \text{cm}$$ باشد، اندازه وتر مثلث را محاسبه کنید.

حل: با توجه به فرمول مساحت مثلث قائم الزاویه، میتوان نوشت:
$$\large A = \frac 12 \times a \times b \Rightarrow 24 = 0.5 \times 6\times b \\
\large \Rightarrow b = \frac {24}{0.5\times 6} = 8 \; \text{cm} $$
اکنون که اندازه ضلع $$b$$ را نیز داریم، میتوانیم به راحتی با استفاده از قضیه فیثاغورس میتوان نوشت:
$$\large a^2+b^2 = c^ 2 \Rightarrow 6 ^2 + 8 ^ 2 = c ^2\\
\large c ^2 = 36+64 = 100 \Rightarrow c = \sqrt{100} = 10 \, \text{cm}$$
معرفی فیلم آموزش هندسه پایه دهم (هندسه ۱) فرادرس
برای آشنایی بیشتر با چندضلعیها و محاسبه مساحت و محیط آنها، پیشنهاد میکنیم به فیلم آموزش هندسه پایه دهم (هندسه ۱) مراجعه کنید که توسط فرادرس تهیه شده است. این آموزش ویدیویی که مدت زمان آن ۴ ساعت و ۳ دقیقه است، در چهار درس تهیه شده است.
در درس اول این آموزش، ترسیمهای هندسی و استدلال معرفی شدهاند. موضوعات درس دوم، به قضیه تالس و تشابه مثلثها و کاربردهای آنها اختصاص یافته است. در درس سوم، مباحث مربوط به چندضلعیها و ویژگیهایی از آنها و همچنین، مساحت و کاربردهای آن مورد بیان شده است. در نهایت، موضوع درس چهارم، تجسم فضایی است که خط، نقطه و صفحه و همچنین تفکر تجسمی را شامل میشود.
- برای مشاهده فیلم آموزش هندسه پایه دهم (هندسه ۱) + اینجا کلیک کنید.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)(همین مطلب)
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + فیلم آموزشی و تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه — به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع