محاسبه طول کمان — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

در آموزش‌های پیشین مجله فرادرس، با انتگرال و روش‌های محاسبه آن آشنا شدیم. در این آموزش، با یکی از کاربردهای انتگرال، یعنی محاسبه طول کمان آشنا می‌شویم.

طول کمان در مختصات قائم

فرض کنید منحنی $$C$$ با رابطه $$y=f(x)$$ تعریف می‌‌شود که در آن $$f$$ روی بازه $$[a,b]$$ پیوسته است.

همچنین، فرض می‌‌کنیم که $$f^\prime\left( x \right)$$ نیز روی بازه $$[a,b]$$ پیوسته باشد.

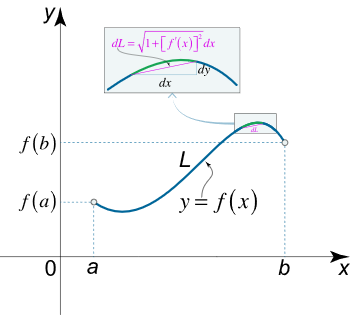
آنگاه، طول منحنی $$y=f(x)$$ از $$x=a$$ تا $$x=b$$ با رابطه زیر به دست می‌‌آید:

$$ \large L = \int \limits _ a ^ b { \sqrt { 1 + { { \left [ { f ^ \prime \left ( x \right ) } \right ] } ^ 2 } } d x } . $$

اگر از نماد لایبنیتس برای مشتق استفاده کنیم، طول کمان با فرمول زیر نشان داده می‌‌شود:

$$ \large L = \int \limits _ a ^ b { \sqrt { 1 + { { \left ( { \frac { { d y } } { { d x } } } \right ) } ^ 2 } } d x } . $$

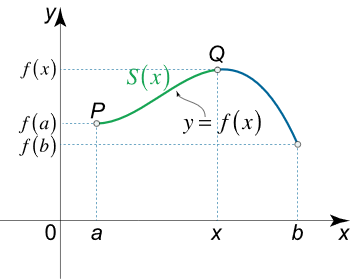
در اینجا تابعی را معرفی می‌‌کنیم که طول کمان یک منحنی را از یک نقطه ثابت منحنی اندازه می‌‌گیرد. فرض کنید $${P_0}\left( {a,f\left( a \right)} \right)$$ نقطه اولیه روی منحنی $$y = f\left( x \right)$$ ($$a \le x \le b$$) باشد، آنگاه طول کمان منحنی از $${P_0}\left( {a,f\left( a \right)} \right)$$ تا نقطه $$Q\left( {x,f\left( x \right)} \right)$$ توسط انتگرال زیر محاسبه می‌‌شود:

$$ \large S \left ( x \right ) = \int \limits _ a ^ x { \sqrt { 1 + { { \left [ { f’ \left ( t \right ) } \right ] } ^ 2 } } d t } , $$

در اینجا $$t$$ متغیر داخلی انتگرال و تابع $$S(x)$$ نیز تابع طول کمان است.

طول کمان منحنی پارامتری

اگر منحنی $$C$$ با معادلات پارامتری زیر نشان داده شود:

$$ \large { x = x \left ( t \right ) , \; \; } \kern0pt { y = y \left ( t \right ) , } $$

که در آن پارامتر $$t$$ بین $$t_1$$ و $$t_2$$ باشد، آنگاه طول کمان منحنی برابر است با:

$$ \large L = \int \limits _ { { t _ 1 } } ^ { { t _ 2 } } { \sqrt { { { \left [ { x’ \left ( t \right ) } \right ] } ^ 2 } + { { \left [ { y’ \left ( t \right ) } \right ] } ^ 2 } } d t } . $$

طول کمان در مختصات قطبی

طول کمان یک منحنی قطبی با رابطه $$r = r\left( \theta \right)$$ که در آن محدوده $$\theta$$ بازه $$\left[ {\alpha ,\beta } \right]$$ است، توسط فرمول زیر به دست می‌‌آید:

$$ \large L = \int \limits _ \alpha ^ \beta { \sqrt { { { \left [ { r \left ( \theta \right ) } \right ] } ^ 2 } + { { \left [ { r ^ \prime \left ( \theta \right ) } \right ] } ^ 2 } } d \theta } . $$

مثال‌ها

در این بخش، چند مثال را بررسی می‌کنیم.

مثال ۱

طول پاره‌‌خط $$y = 7x + 2$$ را از $$x=2$$ تا $$x=6$$ به دست آورید.

حل: ابتدا مسئله را به صورت کلی حل می‌‌کنیم. پاره‌‌خط دلخواهی را در نظر بگیرید که با رابطه $$y = mx+n$$ تعریف می‌‌شود. طول پاره‌‌خط را در بازه $$\left[ {a,b} \right]$$ محاسبه می‌‌کنیم. بدیهی است که

$$ \large { y ^ \prime = f ^ \prime \left ( x \right ) } = { \left ( { m x + n } \right ) ^ \prime } = { m . } $$

با استفاده از فرمول طول کمان، داریم:

$$ \large { L = \int \limits _ a ^ b { \sqrt { 1 + { { \left [ { f’ \left ( x \right ) } \right ] } ^ 2 } } d x } } = { \int \limits _ a ^ b { \sqrt { 1 + { m ^ 2 } } d x } } = { \sqrt { 1 + { m ^ 2 } } \left ( { b – a } \right ) . } $$

بنابراین، طول پاره‌‌خط $$y = 7x + 2$$ برابر است با:

$$ \large { L = \sqrt { 1 + { 7 ^ 2 } } \left ( { 6 – 2 } \right ) } = { 4 \sqrt { 5 0 } } = { 2 0 \sqrt 2 . } $$

مثال ۲

طول کمان سهمی نیم‌مکعبی $$y = {x^{\frac{3}{2}}}$$ را از $$x=0$$ تا $$x=5$$ بیابید.

حل: از فرمول طول کمان استفاده می‌‌کنیم:

$$ \large L = \int \limits _ a ^ b { \sqrt { 1 + { { \left [ { f’ \left ( x \right ) } \right ] } ^ 2 } } d x } . $$

در اینجا $$f\left( x \right) = {x^{\frac{3}{2}}}$$، $$f^\prime\left( x \right) = \left( {{x^{\frac{3}{2}}}} \right)^\prime = \large{\frac{3}{2}}\normalsize{x^{\frac{1}{2}}}$$، $$a=0$$ و $$b=5$$ است. در نتیجه:

$$ \large { L = \int \limits _ 0 ^ 5 { \sqrt { 1 + { { \left ( { \frac { 3 } { 2 } { x ^ { \frac { 1 } { 2 } } } } \right ) } ^ 2 } } d x } } = { \int \limits _ 0 ^ 5 { \sqrt { 1 + \frac { { 9 x } } { 4 } } d x} } = { \frac { 1 } { 2 } \int \limits _ 0 ^ 5 { \sqrt { 4 + 9 x } d x } . } $$

برای حل این انتگرال، روش تغییر متغیر را به کار می‌‌گیریم:

$$ \large { { u ^ 2 } = 4 + 9 x , } \; \; \Rightarrow { u = \sqrt { 4 + 9 x } , } \; \; \Rightarrow { 2 u d u = 9 d x , } \; \; \Rightarrow { d x = \frac { { 2 u d u } } { 9 } . } $$

هنگامی که $$x=0$$ است، $$u=2$$ و هنگامی که $$x=5$$ است، $$u=7$$ خواهد بود. بنابراین، انتگرال به صورت زیر محاسبه می‌‌شود:

$$ \large { L = \frac { 1 } { 2 } \int \limits _ 2 ^ 7 { \left ( { u \cdot \frac { 2 } { 9 } u } \right ) d u } } = { \frac { 1 } { 9 } \int \limits _ 2 ^ 7 { { u ^ 2 } d u } } = { \frac { 1 } { 9 } \cdot \left . { \frac { { { u ^ 3 } } } { 3 } } \right | _ 2 ^ 7 } = { \frac { 1 } { { 2 7 } } \left ( { { 7 ^ 3 } – { 2 ^ 3 } } \right ) } = { \frac { { 3 3 5 } } { { 2 7 } } . } $$

مثال ۳

ثابت کنید که محیط دایره‌‌ای به شعاع $$R$$ برابر با $$2 \pi R $$ است.

حل: ابتدا محیط نیم‌‌دایره بالا را محاسبه کرده و سپس جواب حاصل را در 2 ضرب می‌‌کنیم. نیم‌‌دایره بالا با تابع زیر تعریف می‌‌شود:

$$ \large y = \sqrt { { R ^ 2 } – { x ^ 2 } } . $$

با مشتق گرفتن از این تابع خواهیم داشت:

$$ \large \require {cancel} { y ^ \prime = f ^ \prime \left ( x \right ) } = { \left ( { \sqrt { { R ^ 2 } – { x ^ 2 } } } \right ) ^ \prime } = { – \frac { { \cancel { 2 } x } } { { \cancel { 2 } \sqrt { { R ^ 2 } – { x ^ 2 } } } } } = { – \frac { x } { { \sqrt { { R ^ 2 } – { x ^ 2 } } } } . } $$

بنابراین، محیط دایره برابر است با:

$$ \large \begin {align*}
L & = 2 \int \limits _ { – R } ^ R { \sqrt { 1 + { { \left [ { f’ \left ( x \right ) } \right ] } ^ 2 } } d x } = { 2 \int \limits _ { – R } ^ R { \sqrt { 1 + { { \left ( { – \frac { x } { { \sqrt { { R ^ 2 } – { x ^ 2 } } } } } \right ) } ^ 2 } } d x } } \\ & = { 2 \int \limits _ { – R } ^ R { \sqrt { 1 + \frac { { { x ^ 2 } } }{ { { R ^ 2 } – { x ^ 2 } } } } d x } } = { 2 \int \limits _ { – R } ^ R { \sqrt { \frac { { { R ^ 2 } } } { { { R ^ 2 } – { x ^ 2 } } } } d x } } \\ & = { 2 R \int \limits _ { – R } ^ R { \frac { { d x } } { { \sqrt { { R ^ 2 } – { x ^ 2 } } } } } } = { 2 R \left . { \arcsin \frac { x } { R } } \right | _ { – R } ^ R } \\ &= { 2 R \left [ { \arcsin 1 – \arcsin \left ( { – 1 } \right ) } \right ] } = { 2 R \left [ { \frac { \pi } { 2 } – \left ( { – \frac { \pi } { 2 } } \right ) } \right ] } = { 2 \pi R . }
\end {align*} $$

مثال ۴

طول کمان منحنی $$y = \ln x$$ را از $$x = \sqrt{3}$$ تا $$x = \sqrt{15}$$ محاسبه کنید.

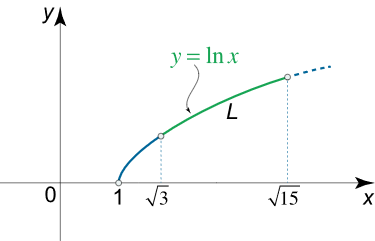
حل:‌ از آنجایی که $$y^\prime = \left( {\ln x} \right)^\prime = \large{\frac{1}{x}}\normalsize$$ است، می‌‌توان نوشت:

$$ \large \begin {align*}
L & = \int \limits _ a ^ b { \sqrt { 1 + { { \left [ { f’ \left ( x \right ) } \right ] } ^ 2 } } d x } = { \int \limits _ { \sqrt 3 } ^ { \sqrt { 1 5 } } { \sqrt { 1 + { { \left ( { \frac { 1 } { x } } \right ) } ^ 2} } d x } } \\ & = { \int \limits _ { \sqrt 3 } ^ { \sqrt { 1 5 } } { \sqrt { \frac { { { x ^ 2 } + 1 } } { { { x ^ 2 } } } } d x } } = { \int \limits _ { \sqrt 3 } ^ { \sqrt { 1 5 } } { \frac { { \sqrt { { x ^ 2 } + 1 } } } { x } d x } . }
\end {align*} $$

برای محاسبه این انتگرال، آن را به صورت زیر بازنویسی می‌‌کنیم:

$$ \large { I = \int { \frac { { \sqrt { { x ^ 2 } + 1 } } } { x } d x } } = { \int { \frac { { x \sqrt { { x ^ 2 } + 1 } } }{ { { x ^ 2 } }} d x } } $$

و از تغییر متغیر استفاده می‌‌کنیم:

$$ \large { { x ^ 2 } + 1 = { u ^ 2 } , } \; \; \Rightarrow { x d x = u d u , } \; \; \Rightarrow { { x ^2 } = { u ^ 2 } – 1 . } $$

در نتیجه:

$$ \large \begin {align*}
I & = \int { \frac { { { u ^ 2 } } } {{ { u ^ 2 } – 1 } } d u } = { \int { \frac { { { u ^ 2 } – 1 + 1 } } { { { u ^ 2 } – 1 } } d u } } = { \int { \left ( { 1 + \frac { 1 } { { { u ^ 2 } – 1 } } } \right ) d u } } \\ &= { u + \frac { 1 } { 2 } \ln \left | { \frac { { u – 1 } } { { u + 1 } } } \right | } = { \sqrt { { x ^ 2 } + 1 } + \frac { 1 } { 2 } \ln \left | { \frac { { \sqrt { { x ^ 2 } + 1 } – 1 } } { { \sqrt { { x ^ 2 } + 1 } + 1 } } } \right | . }
\end {align*} $$

با جایگذاری متغیر قبلی، طول کمان $$L$$ را به دست می‌‌آوریم:

$$ \large \begin {align*}
L & = \kern0pt { \left . { \left [ { \sqrt { { x ^ 2 } + 1 } + \frac { 1 } { 2 } \ln \left | { \frac { { \sqrt { { x ^ 2 } + 1 } – 1 } } { { \sqrt { { x ^ 2 } + 1 } + 1 } } } \right | } \right ] } \right | _ { \sqrt 3 } ^ { \sqrt { 1 5 } } } \\ & = { \left ( { 4 + \frac { 1 } { 2 } \ln \frac { { 4 – 1 } } { { 4 + 1 } } } \right ) – \left ( { 2 + \frac { 1 } { 2 } \ln \frac { { 2 – 1 } } { { 2 + 1 } } } \right ) } \\ & = { 2 + \frac { 1 } { 2 } \left ( { \ln \frac { 3 } { 5 } } - { \ln \frac { 1 } { 3 } } \right ) } = { 2 + \frac { 1 }{ 2 } \ln \frac { 9 } { 5 } . }
\end {align*} $$

مثال ۵

طول کمان منحنی $$y = \ln \sec x$$ را از $$x = 0$$ تا $$x = \large{\frac{\pi }{3}}\normalsize$$ بیابید.

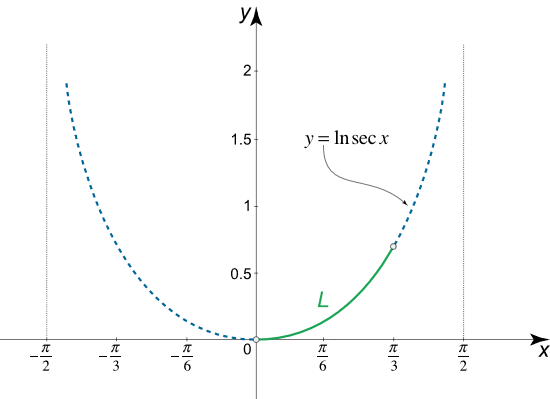
حل: ابتدا از این تابع مشتق می‌‌گیریم:

$$ \large \begin {align*}
y ^ \prime & = f ^ \prime \left ( x \right ) = { \left ( { \ln \sec x } \right ) ^ \prime } = { \frac { 1 } { { \sec x } } \left ( { \sec x } \right ) ^ \prime } \\ & = { \frac { { \left ( { – { { \sec } ^ 2 } x } \right ) \left ( { – \sin x } \right ) } } { { \sec x } } } = { \sec x \sin x } = { \tan x . }
\end {align*} $$

با استفاده از فرمول طول کمان، داریم:

$$ \large \begin {align*}
L & = \int \limits _ a ^ b { \sqrt { 1 + { { \left [ { f’ \left ( x \right ) } \right ] } ^ 2 } } d x } = { \int \limits _ 0 ^ { \frac { \pi } { 3 } } { \sqrt { 1 + { { \tan } ^ 2 } x } d x } } \\ & = { \int \limits _ 0 ^ { \frac { \pi } { 3 } } { \sqrt { { { \sec } ^ 2 } x } d x } } = { \int \limits _ 0 ^ { \frac { \pi } { 3 } } { \sec x d x } . }
\end {align*} $$

از آنجایی که

$$ \large \begin {align*}
\int { \sec x d x } = \ln \left | { \sec x + \tan x } \right | + C ,
\end {align*} $$

خواهیم داشت:

$$ \large \begin {align*}
L & = \kern0pt { \left . { \left [ { \ln \left | { \sec x + \tan x } \right | } \right ] } \right | _ 0 ^ { \frac { \pi } { 3 } } } = { \ln \left | { \sec \frac { \pi } { 3 } + \tan \frac { \pi } { 3 } } \right | } - { \ln \left | { \sec 0 + \tan 0 } \right | } \\ & = { \ln \left ( { 2 + \sqrt 3 } \right ) – \underbrace { \ln \left ( { 1 + 0 } \right ) } _ 0 } = { \ln \left ( { 2 + \sqrt 3 } \right ) . } \end {align*} $$

مثال ۶

طول کمان منحنی نمایی $$y = {e^x}$$ را از $$x=0$$ تا $$x=1$$ به دست آورید.

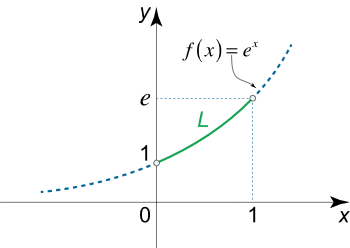
حل: طول کمان این منحنی برابر است با:

$$ \large \begin {align*}
{ L = \int \limits _0 ^ 1 { \sqrt { 1 + { { \left [ { y ^ \prime \left ( x \right ) } \right ] } ^ 2} } d x } } = { \int \limits _ 0 ^ 1 { \sqrt { 1 + { e ^ { 2 x } } } d x } . }
\end {align*} $$

به کمک تغییر متغیر، این انتگرال را به دست می‌‌آوریم:

$$ \large \begin {align*}
& 1 + { e ^ { 2 x } } = { u ^ 2 } , \; \; \Rightarrow { { e ^ { 2 x } } d x = u d u , } \; \; \\& \Rightarrow { d x = \frac { { ud u } }{ { { e ^ { 2 x } } } } = \frac { { u d u } } { { { u ^ 2 } – 1 } } . }
\end {align*} $$

در نتیجه:

$$ \large \begin {align*}
I & = \int { \frac { { {u ^ 2 } d u } } { { { u ^ 2 } – 1 } } } = { \int { \frac { { { u ^ 2 } – 1 + 1 } } { { { u ^ 2 } – 1 } }d u } } = { \int { \left ( { 1 + \frac { 1 } { { { u ^ 2 } – 1 } } } \right ) d u } } \\ & = { u + \frac { 1 } { 2 } \ln \left | { \frac { { u – 1 } } { { u + 1 } } } \right | } = { \sqrt { 1 + { e ^ { 2 x } } } + \frac { 1 } { 2 } \ln \left | { \frac { { \sqrt { 1 + { e ^ { 2 x } } } – 1 } } { { \sqrt { 1 + { e ^ { 2 x } } } + 1 } } } \right | . }
\end {align*} $$

$$ \large \begin {align*}
L & = \kern0pt { \left . { \left [ { \sqrt { 1 + { e ^ { 2 x } } } + \frac { 1 } { 2 } \ln \left | { \frac { { \sqrt { 1 + { e ^ { 2 x} } } – 1 } } { { \sqrt { 1 + { e ^ { 2 x } } } + 1 } } } \right | } \right ] } \right | _ 0 ^ 1 } \\ & = { \left ( { \sqrt { 1 + { e ^ 2 } } + \frac { 1 } { 2 } \ln \frac { { \sqrt { 1 + { e ^ 2 } } – 1 } } { { \sqrt { 1 + { e ^ 2 } } + 1 } } } \right ) } - { \left ( { \sqrt 2 + \frac { 1 } { 2 } \ln \frac { { \sqrt 2 – 1 } } { { \sqrt 2 + 1 } } } \right ) . }
\end {align*} $$

اکنون، کسرهای زیر لگاریتم را ساده می‌‌کنیم:

$$ \large \begin {align*}
\frac { { \sqrt { 1 + { e ^ 2 } } – 1 } } { { \sqrt { 1 + { e ^ 2 } } + 1 } } = { \frac { { { { \left ( { \sqrt { 1 + { e ^2 } } – 1 } \right ) } ^ 2 } } }{ { { { \left ( { \sqrt { 1 + { e ^ 2 } } } \right ) } ^ 2 } – { 1 ^ 2 } } } } = { \frac { { { { \left ( { \sqrt { 1 + { e ^ 2 } } – 1 } \right ) } ^ 2 } } } { { { e ^ 2 } } } } = { { \left ( { \frac { { \sqrt { 1 + { e ^ 2 } } – 1 } } { e } } \right)^2}}
\end {align*} $$

$$ \large { \frac { { \sqrt 2 – 1 } } { { \sqrt 2 + 1 } } } = { \frac { { { { \left ( { \sqrt 2 } \right ) } ^ 2 } – { 1 ^ 2 } } }{ { { { \left ( { \sqrt 2 + 1 } \right ) } ^ 2 } } } } = { { \left ( { \frac { 1 } { { \sqrt 2 + 1 } } } \right ) ^ 2 } . } $$

بنابراین، طول کمان برابر است با:

$$ \large \begin {align*}
L & = \sqrt { 1 + { e ^ 2 } } - { \sqrt 2 } + { \frac { 1 } { 2 } \ln { \left ( { \frac { { \sqrt { 1 + { e ^ 2 } } – 1 } } { e } } \right ) ^ 2 } } - { \frac { 1 } { 2 } \ln { \left ( { \frac { 1 } { { \sqrt 2 + 1 } } } \right ) ^ 2 } } \\& = { \sqrt { 1 + { e ^ 2 } } } - { \sqrt 2 } + { \ln \frac { { \sqrt { 1 + { e ^ 2 } } – 1 } } { e } } - { \ln \frac { 1 } { { \sqrt 2 + 1 } } } \\ & = { \sqrt { 1 + { e ^ 2 } } } - { \sqrt 2 } + { \ln \left [ { \left ( { \sqrt { 1 + { e ^ 2 } } – 1 } \right ) \left ( { \sqrt 2 + 1 } \right ) } \right ] } - { \underbrace { \ln e } _ 1 } \\ &= { \sqrt { 1 + { e ^ 2 } } } - { \sqrt 2 – 1 } + { \ln \left [ { \left ( { \sqrt { 1 + { e ^ 2 } } – 1 } \right ) \left ( { \sqrt 2 + 1 } \right ) } \right ] } \approx {2.004}
\end {align*} $$

مثال ۷

معادلات پارامتری یک چرخزاد به صورت $$x\left( t \right) = t – \sin t$$ و $$y\left( t \right) = 1 – \cos t$$ است. طول یک کمان از آن را محاسبه کنید.

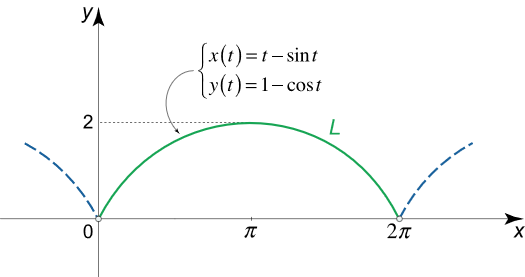
حل: طول کمان یک منحنی پارامتری توسط انتگرال زیر به دست می‌‌آید:

$$ \large L = \int \limits _ { { t _ 1 } } ^ { { t _ 2 } } { \sqrt { { { \left [ { x ^ \prime \left ( t \right ) } \right ] } ^ 2 } + { { \left [ { y ^ \prime \left ( t \right ) } \right ] } ^ 2 } } d t } . $$

برای کمان اول چرخزاد که $$0 \le t \le 2\pi$$ است، داریم:

$$ \large \begin {align*}
L & = \kern0pt { \int \limits _ 0 ^ { 2 \pi } { \sqrt { { { \left ( { 1 – \cos t } \right ) } ^ 2 } + { { \sin } ^ 2 } t } \, d t } } = { \int \limits _ 0 ^ { 2 \pi } { \sqrt { 1 – 2 \cos t + \underbrace { { { \cos } ^ 2 } t + { { \sin } ^ 2 } t } _ 1 } \, d t } } \\ & = { \int \limits _ 0 ^ { 2 \pi } { \sqrt { 2 – 2 \cos t } \, d t } } = { \int \limits _ 0 ^ { 2 \pi } { \sqrt { 4 { { \sin } ^ 2 } \frac { t } { 2 } } d t } } = { 2 \int \limits _ 0 ^ { 2 \pi } { \sin \frac { t } { 2 } d t } } = { 4 \left . { \left ( { – \cos \frac { t } { 2 } } \right ) } \right | _ 0 ^ { 2 \pi } } \\ & = { 4 \left ( { – \cos \pi + \cos 0 } \right ) } = { 8 . }
\end {align*} $$

مثال ۸

طول کمان یک خم ستاره‌‌ای را که معادلات آن به صورت $$x\left( t \right) = {\cos ^3}t$$ و $$y\left( t \right) = {\sin^3}t$$ هستند، محاسبه کنید.

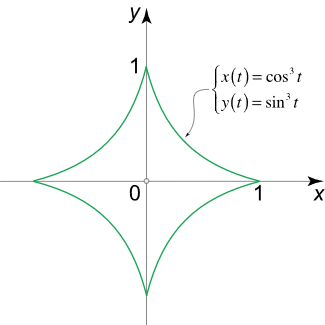
حل: معادلات این منحنی را به صورت پارامتری می‌نویسیم. بنابراین، از فرمول زیر استفاده می‌‌کنیم:

$$ \large { L \text { = } } \kern0pt { \int \limits _ a ^ b { \sqrt { { { \left [ { x ^ \prime \left ( t \right ) } \right ] } ^ 2 } + { { \left [ { y ^ \prime \left ( t \right ) } \right ] } ^ 2 } } d t } . } $$

مشتق معادلات پارامتری به صورت زیر است:

$$ \large { x ^ \prime \left ( t \right ) = \left ( { { { \cos } ^ 3 } t } \right ) ^ \prime } = { 3 { \cos ^ 2 } t \left ( { – \sin t } \right ) } = { – 3 { \cos ^ 2 } t \sin t , } $$

$$ \large { y ^ \prime \left ( t \right ) = \left ( { { { \sin } ^ 3 } t } \right ) ^ \prime } = { 3 { \sin ^ 2 } t \cos t . } $$

طول یک کمان از خم ستاره‌‌ای واقع در ربع اول را محاسبه کرده، سپس جواب به دست آمده را در 4 ضرب می‌‌کنیم. بنابراین، خواهیم داشت:

$$ \large \begin {align*}
L & = \kern0pt { 4 \int \limits _ 0 ^ { \frac { \pi } { 2 } } { \sqrt { 9 \, { { \cos } ^ 4 } t \, { { \sin } ^ 2 } t + 9 \, { { \sin } ^ 4 } t \, { { \cos } ^ 2 } t } \, d t } } \\ &= { 4 \int \limits _ 0 ^ { \frac { \pi } {2 } } { \sqrt { 9 \, { { \sin } ^ 2 } t \,{ { \cos } ^ 2 } t \underbrace { \left ( { { { \cos } ^ 2 } t + { { \sin } ^ 2 } t } \right ) } _ 1 } d t } } \\& = { 1 2 \int \limits _ 0 ^ { \frac { \pi } { 2 } } { \sin t \cos t d t } } = { 6 \int \limits _ 0 ^ { \frac { \pi } { 2 } } { \sin 2 t d t } } \\ & = { – 3 \left . { \cos 2 t } \right | _ 0 ^ { \frac { \pi } { 2 } } } = { – 3 \left ( { \cos \pi – \cos 0 } \right ) } = { 6 . }
\end {align*} $$

مثال ۹

طول یک دلوار را که معادله آن به صورت $$r = 1 + \cos \theta$$ است، بیابید.

حل: دلوار را در مختصات قطبی تعریف می‌‌کنیم. از این رو، از فرمول زیر استفاده خواهیم کرد:

$$ \large L = \int \limits _ \alpha ^ \beta { \sqrt { { { \left [ { r \left ( \theta \right ) } \right ] } ^ 2 } + { { \left [ { r ^ \prime \left ( \theta \right ) } \right ] } ^ 2 } } d \theta } . $$

به دلیل تقارن، طول کمان نیمه بالایی دلوار را محاسبه می‌‌کنیم (بازه $$\theta$$ از $$0$$ تا $$\pi$$ است) و نتیجه را در 2 ضرب می‌‌کنیم. بنابراین، خواهیم داشت:

$$ \large \begin {align*}
L & = \int \limits _ \alpha ^ \beta { \sqrt { { { \left [ { r \left ( \theta \right ) } \right ] } ^ 2 } + { { \left [ { r’ \left ( \theta \right ) } \right ] } ^ 2 } } d \theta } = { 2 \int \limits _ 0 ^ \pi { \sqrt { { { \left ( { 1 + \cos \theta } \right ) } ^ 2 } + { { \left ( { – \sin \theta } \right ) } ^ 2 } } d \theta } } \\ &= { 2 \int \limits _ 0 ^ \pi { \sqrt { 1 + 2 \cos \theta + \underbrace { { { \cos } ^ 2 } \theta + { { \sin } ^ 2 } \theta } _ 1 } \, d \theta } } = { 2 \int \limits _ 0 ^ \pi { \sqrt { 2 + 2 \cos \theta } \, d \theta } } \\ & = { 2 \sqrt 2 \int \limits _ 0 ^ \pi { \sqrt { 1 + \cos \theta } \, d \theta } } = { 2 \sqrt 2 \int \limits _ 0 ^ \pi { \sqrt { 2 { { \cos } ^ 2 } \frac { \theta } { 2 } } d \theta } } \\ &= { 4 \int \limits _ 0 ^ \pi { \cos \frac { \theta } { 2 } d \theta } } = { 8 \left . { \sin \frac { \theta } { 2 } } \right | _ 0 ^ \pi } = { 8 \left ( { \sin \frac { \pi } { 2 } – \sin 0 } \right ) } = { 8 . }
\end {align*} $$

مثال ۱۰

طول دور اول مارپیچ ارشمیدس $$r\left( \theta \right) = \theta$$ را به دست آورید.

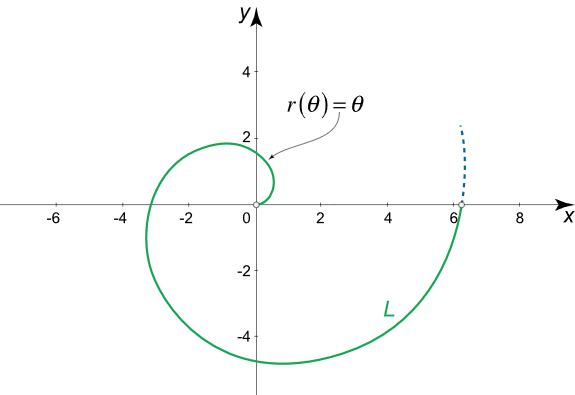
حل: طول کمان یک منحنی در مختصات قطبی از رابطه زیر به دست می‌‌آید:

$$ \large L = \int \limits _ \alpha ^ \beta { \sqrt { { { \left [ { r \left ( \theta \right ) } \right ] } ^ 2 } + { { \left [ { r ^ \prime \left ( \theta \right ) } \right ] } ^ 2 } } d \theta } . $$

در اینجا $$\alpha = 0$$، $$\beta = 2\pi$$، $$r\left( \theta \right) = \theta$$ و $$r^\prime\left( \theta \right) = 1$$ است. در نتیجه، این انتگرال به صورت زیر خواهد بود:

$$ \large L = \int \limits _ 0 ^ { 2 \pi } { \sqrt { 1 + { \theta ^ 2 } } d \theta } . $$

برای به دست آوردن جواب انتگرال از تغییر متغیر مثلثاتی $$\theta = \tan t$$ استفاده می‌‌کنیم. با جایگذاریِ

$$ \large { \theta = \tan t , \; \; } \kern0pt { \sqrt { 1 + { \theta ^ 2 } } = \sec t , \; \; } \kern0pt { d \theta = { \sec ^ 2 } t \, d t , } $$

انتگرال نامعین را به شکل زیر بازنویسی می‌‌کنیم:

$$ \large { I = \int { \sqrt { 1 + { \theta ^ 2 } } d \theta } } = { \int { { { \sec } ^ 3 } t d t } . } $$

انتگرال حاصل برابر است با:

$$ \large { \int { { { \sec } ^ 3 } t d t } } = { \frac { { \sec t \tan t } } { 2 } } + { \frac { 1 } { 2} \int { \sec t d t } . } $$

از طرفی، داریم:

$$ \large \int { \sec t d t } = \ln \left | { \sec t + \tan t } \right | . $$

در نتیجه:

$$ \large { \int { { { \sec } ^ 3 } t d t } } = { \frac { { \sec t \tan t } } { 2 } } + { \frac { 1 } { 2 } \ln \left | { \sec t + \tan t } \right | . } $$

با جایگذاری متغیر قبلی، خواهیم داشت:

$$ \large { I = \frac { { \theta \sqrt { 1 + { \theta ^ 2 } } } } { 2 } } + { \frac { 1 } { 2 } \ln \left | { \sqrt { 1 + { \theta ^ 2 } } + \theta } \right | . } $$

بنابراین، طول کمان برابر است با:

$$ \large \begin {align*} \require {cancel}
L & = \kern0pt { \left . { \left [ { \frac { { \theta \sqrt { 1 + { \theta ^ 2 } } } } { 2 } + \frac { 1 } { 2 } \ln \left | { \sqrt { 1 + { \theta ^ 2 } } + \theta } \right | } \right ] } \right | _ 0 ^ { 2 \pi } } \\ & = { \left ( { \frac { { \cancel { 2 } \pi \sqrt { 1 + 4 { \pi ^ 2 } } } } { \cancel { 2 } } } \right . } + { \left . { \frac { 1 } { 2 } \ln \left | { \sqrt { 1 + 4 { \pi ^ 2 } } + 2 \pi } \right | } \right ) } - { \underbrace { \left ( { 0 + \frac { 1 }{ 2 } \ln 1 } \right ) } _ 0 } \\ & = { \pi \sqrt { 1 + 4 { \pi ^ 2 } } + \frac { 1 } { 2 } \ln \left ( { \sqrt { 1 + 4 { \pi ^ 2 } } + 2 \pi } \right ) } \approx { 2 1 . 2 6 }
\end {align*} $$

اگر به یادگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• کاربردهای انتگرال خطی — همراه با مثال
• انتگرال معین — از صفر تا صد
• تقلب نامه (Cheat Sheet) فرمول های انتگرال

^^