سیستم پسیو در مهندسی کنترل — به زبان ساده

۳۴۸ بازدید

آخرین به‌روزرسانی: ۱۳ اردیبهشت ۱۴۰۲

زمان مطالعه: ۱۶ دقیقه

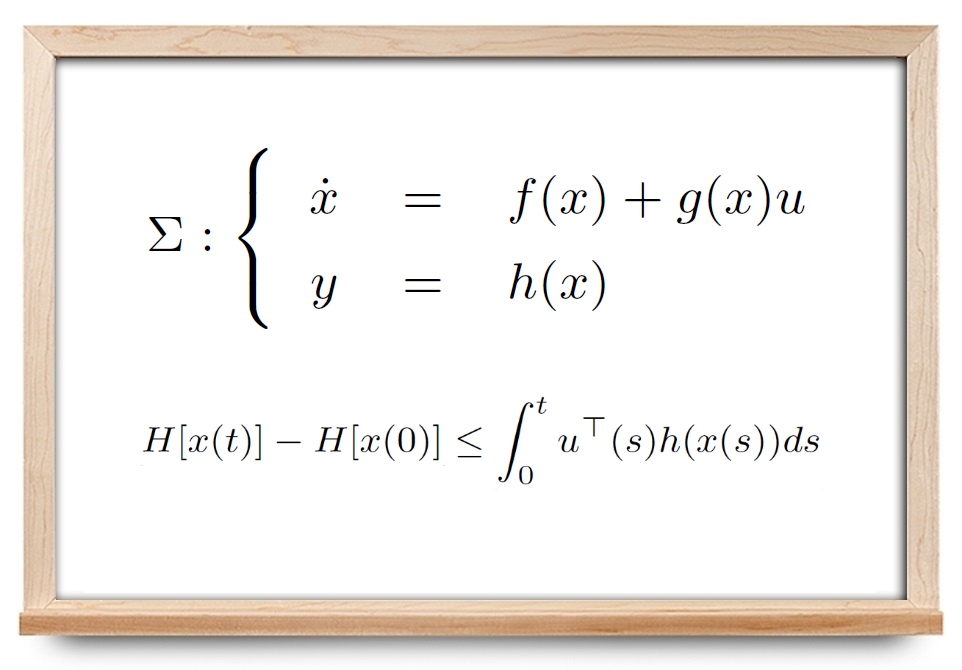
سیستم پسیو در مهندسی کنترل — به زبان ساده

کنترل پسیویتی (Passivity Control)‌ یا کنترل انفعالی کاربرد زیادی در کنترل سیستم‌های غیرخطی دارد. در این آموزش با مفهوم پسیویتی و سیستم پسیو در مهندسی کنترل آشنا می‌شویم.

فهرست مطالب این نوشته

توان و انرژی: سیستم‌های پسیو

تعاریف مربوط به سیستم پسیو

اتصال سیستم‌های پسیو

توان و انرژی: سیستم‌های پسیو

پسیو بودن یک سیستم را ابتدا در قالب نظریه مدار توضیح خواهیم داد. طبق قوانین فیزیک می‌دانیم که توان، نرخ زمانی تغییر انرژی جذب شده یا مصرف شده است:

$$ \large p ( t ) = \frac { d w ( t ) } { d t } \;\;\;\;\; ( 1 ) $$

فیلم آموزش تحلیل سیستم های غیر خطی در فرادرس

کلیک کنید

که در آن، $$ p ( . ) $$ توان، $$ w ( . ) $$ انرژی و $$ t $$ زمان است.

رابطه بالا را می‌توان به فرم انتگرالی زیر نوشت:

$$ \large w ( t ) = \int _ { t _ 0 } ^ t { p ( t ) d t} . \;\;\;\;\; ( 2 ) $$

اکنون یک عنصر اساسی مدار را در نظر بگیرید که با یک جعبه سیاه در شکل ۱ نشان داده شده است.

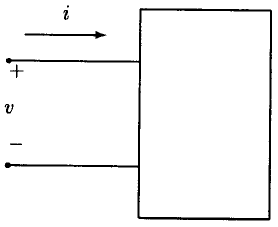
در شکل ۱، ولتاژ‌ دو سر ترمینال‌های جعبه با $$ v $$ و جریان گذرنده از عنصر مداری با $$ i $$ مشخص شده است. انتخاب پلاریته ولتاژ‌ و جهت مرجع جریان کاملاً دلخواه است. توان به صورت زیر نوشته می‌شود:

$$ \large p ( t ) = v ( t ) i ( t ) \;\;\;\;\; ( 3 ) $$

بنابراین، انرژی جذب شده توسط مدار در زمان $$ t$$ برابر است با:

$$ \large w ( t ) = \int _ { - \infty } ^ { t } v ( t ) i ( t ) \mathrm { d } t = \int _ { - \infty } ^ { 0 } v ( t ) i ( t ) \mathrm { d } t + \int _ { 0 } ^ { t } v ( t ) i ( t ) \mathrm { d } t \;\;\;\;\; ( 4 ) $$

جمله اول سمت راست معادله (۴) اثر شرایط اولیه مختلف را در لحظه صفر روی عناصر مدار نشان می‌دهد. با توجه به علامت‌های قراردادی مشخص شده، می‌توان گفت:

(الف) اگر $$ w ( t ) > 0 $$، جعبه انرژی جذب می‌کند (برای مثال می‌توانیم آن را یک مقاومت در نظر بگیریم).
(ب) اگر $$ w ( t ) < 0 $$، جعبه انرژی تحویل می‌دهد (برای مثال، می‌توانیم آن را یک باتری با ولتاژ‌ منفی نسبت به پلاریته مشخص شده در شکل ۱ در نظر بگیریم).

در نظریه مدار، عناصری که انرژی‌شان را خودشان تولید نمی‌کنند، «پسیو» (Passive) می‌نامند، یعنی یک عنصر مداری پسیو است اگر

$$ \large \int _ { - \infty } ^ { t } v ( t ) i ( t ) \mathrm { d } t \geq 0 . \;\;\;\;\; ( 5 ) $$

مقاومت‌ها، خازن‌ها و سلف‌ها در این شرط صدق می‌کنند و بنابراین، «عناصر پسیو» (Passive Elements) نامیده می‌شوند. به طور کلی، خوش‌رفتاری شبکه‌های پسیو تعبیر کاملاً مبهمی دارد. در واقع، بیان مفهوم رفتار خوب در چارچوب نظریه شبکه‌ها یا سیستم‌ها کار آسان و سرراستی نیست. از طرف دیگر، پایداری، به اَشکال مختلف، مفهومی است که برای توصیف یک ویژگی مطلوب سیستم فیزیکی به کار رفته و برای بیان دقیق مفهوم یک سیستم خوش‌رفتار در نظر گرفته می‌شود.

اگر مفهوم پسیویتی در شبکه‌ها مورد استفاده قرار گیرد، باید قادر باشیم توصیفاتی را از یک سیستم پسیو ارائه دهیم. برای بررسی این گزاره، مدار شکل ۲ را در نظر می‌گیریم و فرض می‌کنیم جعبه سیاه شامل یک عنصر مداری پسیو (یا خطی) است.

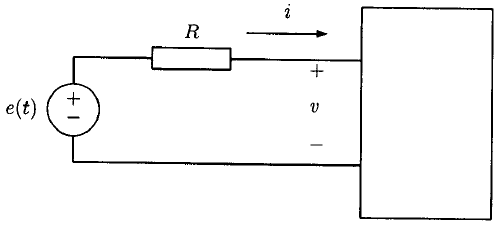
با فرض اینکه شبکه از ابتدا در حالت استراحت (سکون)‌ بوده است، و با استفاده از قانون ولتاژ کیرشهف، داریم:

$$\large e ( t ) = i ( t) R + v ( t ) $$

اکنون فرض کنید یک منبع نیروی محرکه مغناطیسی (emf) که با $$ e ( \cdot ) $$ مشخص شده داریم، به گونه‌ای که

$$\large \int _{ 0 } ^ { T } e ^ { 2 } ( t ) \mathrm { d } t < \infty $$

حاصل انتگرال برابر است با:

$$ \large \begin {aligned}
\int _ { 0 } ^ { T } e ^ { 2 } ( t ) \mathrm{ d } t & = \int _ { 0 } ^ { T } ( i ( t ) R + v ( t ) ) ^ { 2 } \mathrm { d } t \\
& = R ^ { 2 } \int _ { 0 } ^ { T } i ^ { 2 } ( t ) \mathrm { d } t + 2 R \int _ { 0 } ^ { T } i ( t ) v ( t ) \mathrm { d } t + \int _ { 0 } ^ { T } v ^ { 2 } ( t ) \mathrm { d } t
\end {aligned} $$

از آنجا که جعبه سیاه پسیو است، $$ \int _ 0 ^ T { i ( t ) v ( t) } \, dt > 0 $$ خواهد بود. بنابراین، نامساوی زیر را نتیجه می‌گیریم:

$$ \large \int _ { 0 } ^ { T } e ^ { 2 } ( t ) \mathrm { d } t \geq R ^ { 2 } \int _ { 0 } ^ { T } i ^ { 2 } ( t ) \mathrm { d } t + \int _ { 0 } ^ { T } v ^ { 2 } ( t ) \mathrm { d } t $$

علاوه بر این، از آنجا که ولتاژ‌ اعمالی به گونه‌ای است که $$ \int _ 0 ^ \infty e ^ 2 ( t) \, d t < \infty $$، می‌توانیم حد $$ T \to \infty $$ را در دو طرف نامساوی اعمال کنیم. در نتیجه این کار، داریم:

$$ \large R ^ { 2 } \int _ { 0 } ^ { \infty } i ( t ) ^ { 2 } \mathrm { d } t + \int _ { 0 } ^ { \infty } v ^ { 2 } ( t ) \mathrm { d } t \leq \int _ { 0 } ^ { \infty} e ^ { 2 } ( t ) \mathrm { d } t < \infty $$

که بیان می‌کند هم $$ v $$ و هم $$ i$$ انرژی محدودی دارند. از این موضوع این نکته استنباط می‌شود که انرژی این دو کمیت را می‌توان با منبع ورودی $$ e ( \cdot ) $$ کنترل کرد و با این دیدگاه می‌توانیم بگوییم سیستم خوش‌رفتار است. در بخش بعد، نکاتی را که بیان کردیم، در چارچوب نظریه سیستم‌های ورودی-خروجی فرمول‌بندی می‌کنیم و این مفاهیم را برای دسته‌های دیگر سیستم‌ها تعمیم می‌دهیم.

تعاریف مربوط به سیستم پسیو

قبل از آنکه مفهوم پسیویتی را تعریف کرده و برخی از ویژگی‌های آن را مطالعه کنیم، لازم است چند پیش‌نیاز ریاضی و نمادگذاری را ارائه کنیم. ابزار ضروری که در تعریف پسیویتی نیاز داریم فضای ضرب داخلی است.

فیلم آموزش سیستم های کنترل غیر خطی با رویکرد حل مساله در فرادرس

کلیک کنید

تعریف ۱: فضای برداری حقیقی $$ \mathcal{X} $$ را یک فضای ضرب داخلی حقیقی می‌نامیم، اگر برای هر دو بردار $$ x , y \in \mathcal { X}$$، عدد حقیقی $$ \langle x, y\rangle $$ به گونه‌ای وجود داشته باشد که در شرایط زیر صدق کند:

(الف) $$ \langle x , y \rangle = \langle y , x \rangle $$
(ب) $$ \langle x + y , z \rangle = \langle x , z \rangle + \langle y + z \rangle \quad \forall x , y , z \in \mathcal { X } $$
(پ) $$ \langle \alpha x , y \rangle = \alpha \langle y , x \rangle \quad \forall x , y \in \mathcal { X } , \forall \alpha \in \mathbb { R } $$
(ت) $$ \langle x , x \rangle \geq 0 $$
(ث) $$ \langle x , x \rangle = 0 $$ اگر و تنها اگر $$ x = 0 $$

تابع $$ \langle \cdot , \cdot \rangle : \mathcal { X } \times \mathcal { X } \to \mathbb{ R} $$ یک ضرب داخلی از فضای $$ \mathcal { X }$$ نامیده می‌شود. اگر فضای $$ \mathcal { X }$$ کامل باشد، آنگاه فضای ضرب داخلی یک «فضای هیلبرت» (Hilbert Space)‌ نامیده می‌شود. با استفاده از این ویژگی‌ها، می‌توانیم یک نُرم برای هر عنصر از فضای $$ \mathcal { X } $$ به صورت زیر تعریف کنیم:

$$\large || x || _ \mathcal { X } ^ 2 = \langle x ,x \rangle . $$

یک ویژگی مهم فضای ضرب داخلی، «نامساوی شوارتز» (Schwarz inequality) است:

$$\large | \langle x , y \rangle | \leq \| x \| x \| y \| _ { \mathcal { X } } \quad \forall x , y \in \mathcal { X }\;\;\;\;\; ( 6 ) $$

در ادامه، فرض می‌کنیم $$ \mathcal { X } $$ یک فضای ضرب داخلی باشد.

مثال ۱: فرض کنید بُعد $$ \mathcal { X } $$ برابر با $$R ^ n $$ باشد. ضرب نقطه‌ای در $$\mathbb{R}^ n $$ که به صورت زیر تعریف می‌شود:

$$ \large x \cdot = x ^ T y = x _ 1 y _ 1 + x _ 2 y _ 2 + \cdots + x _ n y _ n $$

یک ضرب داخلی در $$ \mathbb { R}^ n $$ تعریف می‌کند. به سادگی می‌توان این موضوع را برای $$ ( i ) $$ و $$ ( v ) $$ تأیید کرد.

تمرکز ما بر سیستم‌های زمان‌پیوسته است. معمولاً در این سیستم‌ها از ضرب داخلی زیر استفاده می‌شود:

$$ \large \langle x , y \rangle = \int _ { 0 } ^ { \infty } x ( t ) \cdot y ( t ) \mathrm { d } t \;\;\;\;\; ( 7 )$$

که $$ x \cdot y $$ ضرب نقطه‌ای عادی است و معمولاً با نام ضرب داخلی طبیعی در $$ \mathcal { L } ^ 2 $$ شناخته می‌شود. در واقع، با این ضرب داخلی، $$ \mathcal { X} = \mathcal {L}_2$$ را داریم و علاوه بر آن:

$$\large \| x \| _ { \mathcal { L } _ { 2 } } ^ { 2 } = \langle x , x \rangle = \int _ { 0 } ^ { \infty } \| x ( t ) \| _ { 2 } ^ { 2 } \mathrm { d } t \;\;\;\;\; ( 8 ) $$

در ادامه، لازم است فضای $$ \mathcal { X } $$ را گسترش دهیم و فرض می‌کنیم ضرب داخلی در رابطه زیر صدق می‌کند:

$$ \large \left \langle x _ { T } , y \right \rangle = \left \langle x , y _ { T } \right \rangle = \left \langle x _ { T } , y _ { T } \right \rangle \stackrel { \text {def}} { = } \langle x , y \rangle _ { T } \;\;\;\;\; ( 9 ) $$

مثال ۲: فرض کنید $$ \mathcal { X } = \mathcal { L } _ 2 $$ فضای توابع انرژی محدود است:

$$ \large \mathcal { X } = \{ x : \mathbb { R } \rightarrow \mathbb { R } \} $$

و در رابطه زیر صدق می‌کند:

$$ \large \| x \| _ { \mathcal { L } _ { 2 } } ^ { 2 } = \langle x , x \rangle = \int _ { 0 } ^ { \infty } x ^ { 2 } ( t ) \mathrm { d } t < \infty $$

بنابراین، $$ \mathcal { X } _ e = \mathcal { L } _ { 2 e} $$ فضای همه توابعی است که «بُرش» (Truncation) یا ترانکشن $$ x _ T $$ متعلق به $$ \mathcal { L } _ 2 $$ باشد، فارغ از اینکه خود $$ x ( t) $$ به $$ \mathcal { L}_2 $$ تعلق داشته باشد. برای مثال، تابع $$ x ( t) = e ^ t $$ به $$ \mathcal { L } _ { 2 e } $$ تعلق دارد، در صورتی که خودش به $$ \mathcal {L}_2 $$ متعلق نیست.

تعریف ۲ (پسیویتی): سیستم $$ H : \mathcal { X} _ e \to \mathcal { X} _ e $$ را پسیو می‌گوییم، اگر

$$ \large \langle u , H u \rangle _ { T } \geq \beta \quad \forall u \in \mathcal { X } _ { e } , \forall T \in \mathbb { R } ^ { + }.
\;\;\;\;\; ( 1 0 ) $$

تعریف ۳ (پسیویتی اکید): سیستم $$ H : \mathcal { X} \to \mathcal { X} _ e $$ را اکیداً پسیو می‌گوییم، اگر $$ \delta > 0 $$ وجود داشته باشد، به گونه‌ای که

$$\large \langle u , H u \rangle _ { T } \geq \delta \left\| u _ { T } \right \| _ { \mathcal { X } } ^ { 2 } + \beta \quad \forall u \in \mathcal { X } _ { e } , \forall T \in \mathbb { R } ^ { + } . \; \; \; \; \; ( 11 ) $$

ثابت $$ \beta $$ در تعاریف ۲ و ۳ یک جمله بایاس است که برای در نظر گرفتن اثر ممکن انرژی ذخیره شده اولیه در زمان $$ t = 0 $$ در نظر گرفته شده است. تعریف ۲ بیان می‌کند که تنها مقدار محدودی از انرژی ذخیره شده در حالت اولیه در $$t = 0 $$ را می‌توان از یک سیستم پسیو استخراج کرد. برای درک بهتر این موارد، به شبکه مثالی که بررسی کردیم بر می‌گردیم.

مثال ۳: مجدداً شبکه شکل ۱ را در نظر بگیرید. برای تحلیل این شبکه به عنوان یک سیستم «مجرد» (Abstract) با ورودی $$ u$$ و خروجی $$ y = H u $$، تعریف می‌کنیم:

$$ \large \begin {align*}
u & = v ( t) \\
y & = H u = i ( t) .
\end {align*} $$

براساس تعریف ۲، شبکه پسیو است اگر و تنها اگر

$$ \large \langle x , H x \rangle _ { T } = \langle v ( t ) , i ( t ) \rangle _ { T } \geq \beta . $$

با انتخاب ضرب داخلی به عنوان ضرب داخلی در $$ \mathcal { L } _ 2 $$، نامساوی اخیر معادل با عبارت زیر است:

$$ \large \int _ { 0 } ^ { T } x ( t ) y ( t ) \mathrm { d } t = \int _ { 0 } ^ { T } v ( t ) i ( t ) \mathrm { d } t \geq \beta \quad \forall v ( t ) \in \mathcal { X } _ { e } , \forall T \in \mathbb { R } . $$

از معادله (۴) می‌دانیم که کل انرژی جذب شده توسط شبکه در زمان $$ t $$ برابر است با:

$$ \large \begin {aligned}
\int _ { - \infty } ^ { t } v ( t ) i ( t ) \mathrm { d } t & = \int _ { 0 } ^ { t } v ( t ) i ( t ) \mathrm { d } t + \int _ { -\infty } ^ { 0 } v ( t ) i ( t ) \mathrm { d } t \\
& = \langle v ( t ) , i ( t ) \rangle _ { T } + \int _ { -\infty } ^ { 0 } v ( t ) i ( t ) \mathrm { d } t
\end {aligned} $$

بنابراین، بر اساس تعریف ۲، شبکه پسیو است اگر و تنها اگر

$$ \large \langle v ( t ) , i ( t ) \rangle _ { T } \geq \beta \stackrel { \text { def }} { = } - \int _ { - \infty } ^ { 0 } v ( t ) i ( t ) \mathrm { d } t $$

تعریف ۴: سیستم $$ H : \mathcal { X } \to \mathcal { X} $$ را اکیداً مثبت می‌گوییم اگر $$ \delta > 0 $$ به گونه‌ای وجود داشته باشد که

$$ \large \langle u , H u \rangle \geq \delta \| u \| _ { X } ^ { 2 } + \beta \quad \forall u \in \mathcal { X } \;\;\;\;\; ( 1 2 ) $$

همچنین، $$H$$ را مثبت می‌گوییم اگر با $$ \delta = 0 $$ در (۱۲) صدق کند.

تنها تفاوت بین مفاهیم پسیویتی و مثبت بودن (اکیداً پسیو و اکیداً مثبت) نبود برش در (۱۲) است. در نتیجه، نمادگذاری مثبت بودن و اکیداً مثبت بودن به طور خاص به سیستم‌های پایدار ورودی-خروجی اعمال می‌شود.

قضیه زیر نشان می‌دهد که اگر سیستم (الف) علّی و (ب) پایدار باشد، آنگاه مفاهیم مثبت بودن و پسیویتی کاملاً معادل هستند.

قضیه ۱: سیستم $$ H : \mathcal { X } \to \mathcal { X} $$ را در نظر بگیرید، و فرض کنید $$H$$ علی باشد. داریم:

(الف) $$ H $$ مثبت است اگر و تنها اگر پسیو باشد.
(ب) $$ H $$ اکیداً‌ مثبت است اگر و تنها اگر اکیداً پسیو باشد.

اثبات: ابتدا فرض کنید که $$H$$ در (۱۲) صدق می‌کند و ورودی دلخواه $$ u \in \mathcal { X } _ e $$ را در نظر بگیرید. در نتیجه، $$ u _ T \in \mathcal { X} $$، و با توجه به (۱۲)، داریم:

$$ \large \left \langle u _ { T } , H u _ { T } \right \rangle \geq \delta \left \| u _ { T } \right\| _ { \mathcal { X } } ^ { 2 } + \beta $$

اما، با توجه به (۹)، خواهیم داشت:

$$ \large \left\langle u _ { T } , H u_ { T } \right \rangle = \left\langle u _ { T } , \left ( H u _ { T } \right ) _ { T } \right \rangle $$

و از آنجا که $$H$$ علّی است، می‌توان نوشت:

$$ \large \left\langle u _ { T } , H u_ { T } \right \rangle = \left \langle u _ { T } , ( H u ) _ { T } \right \rangle $$

و با توجه به (۹)، داریم:

$$ \large \left\langle u _ { T } , H u_ { T } \right \rangle = \left \langle u , H u \right \rangle _ T $$

در نتیجه، $$ \langle u , H u \rangle _ { T } \geq \delta \left \| u _ { T } \right \| ^ { 2 } $$ و از آنجا که $$ u \in \mathcal { X} _ e $$ دلخواه است، نتیجه می‌گیریم که تساوی (۱۱)، معادله (۱۲) را حاصل می‌کند. در مقابل، فرض می‌کنیم $$ H $$ در (۱۱) صدق می‌کند و ورودی دلخواه $$ u \in \mathcal { X} $$ را در نظر می‌گیریم. با توجه به (۱۱)، داریم:

$$ \large \langle u , H u \rangle _ { T } \geq \delta \left \| u _ { T } \right \| _ { \mathcal { X } } ^ { 2 } + \beta $$

اما، از طرفی:

$$ \large \begin {aligned}
\langle u , H u \rangle _ { T } & = \left \langle u _ { T } , ( H u ) _{ T } \right \rangle \\
& = \left \langle u _ { T } , \left ( H u _ { T } \right )_ { T } \right \rangle \\
& = \left \langle u _ { T } , H u _ { T } \right \rangle
\end {aligned} $$

بنابراین، $$ \begin {equation} \left \langle u _ { T } , H u _ { T } \right \rangle \geq \left \| u _ { T } \right\| ^ { 2 } + \beta \end {equation} $$، که برای همه $$T\in \mathbb{R}^+$$ برقرار است. علاوه بر این، از آنجا که $$ u \in \mathcal { X} $$ و $$ H: \mathcal{X} \to \mathcal {X} $$، می‌توانیم حد $$ T \to \infty$$ را اعمال کنیم و خواهیم داشت:

$$ \large \langle u , H u \rangle \geq \delta \left \| u \right \| _ { \mathcal { X } } ^ { 2 } + \beta. $$

بنابراین، تساوی (۱۱)، معادله (۱۲) را نتیجه می‌دهد و بخش دوم قضیه نیز اثبات می‌شود. بخش (الف) نیز به سادگی با فرض $$ \delta = 0 $$ اثبات می‌شود. بنابراین، اثبات قضیه کامل است.

اتصال سیستم‌های پسیو

بسیاری از موقع لازم است ویژگی‌های ترکیب چند سیستم پسیو را بررسی کنیم. قضیه زیر، دو مورد مهم از این ترکیب‌ها را بیان می‌کند.

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

قضیه ۲: تعداد محدودی سیستم $$ H _ i : \mathcal { X } _ e \to \mathcal { X} _ e , i = 1 , ... , n $$ را در نظر بگیرید.

(الف) اگر همه سیستم‌های $$ H _ i , i = 1 , ... , n $$ پسیو باشند، آنگاه سیستم $$ H : \mathcal { X} _ e \to \mathcal { X} _ e $$ که به صورت زیر تعریف می‌شود (شکل ۳)، پسیو است:

$$ \large H = H _ 1 + \cdots + H _ n \quad \quad ( 13 ) $$

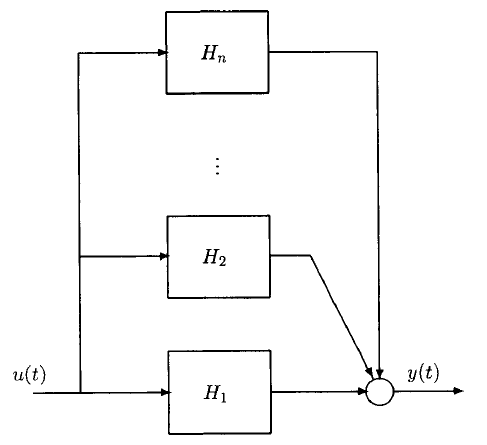
شکل ۳: $$ H = H _ 1 + H _ 2 + \cdots + H _ n $$

(ب) اگر همه سیستم‌های $$ H _ i , i = 1 , ... , n $$ پسیو باشند و حداقل یکی از آن‌ها اکیداً پسیو باشد، آنگاه $$ H$$ که طبق معادله (۱۳) تعریف شده، اکیداً پسیو خواهد بود.
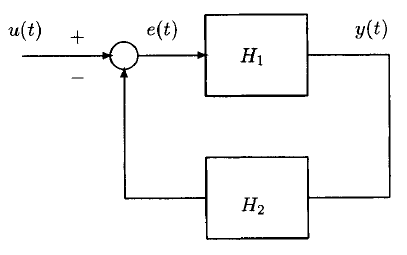
(پ) اگر سیستم‌های $$ H _ i , i = 1 , 2 $$ پسیو باشند و اتصال فیدبکی که با معادلات زیر (شکل ۴) تعریف شده باشد:

$$ \large e = u - H _ 2 y \quad \quad ( 14) $$

$$ \large y = H _ 1 e \quad \quad ( 15) $$

خوش‌تعریف باشد (یعنی $$ e ( t ) \in \mathcal { X} _ e $$ و به صورت یکتا برای هر $$ u ( t) \in \mathcal { X} _ e $$ تعیین شده باشد)، آنگاه تصویر $$ u $$ به $$ y $$ که با معادلات (۱۴)‌ و (۱۵) تعریف شده، پسیو خواهد بود.

اثبات: ابتدا (الف) را اثبات می‌کنیم. رابطه زیر را داریم:

$$ \large \begin {equation} \begin {aligned}
\left \langle x , \left ( H _ { 1 } + \cdots + H _ { n } \right ) x \right \rangle _ { T } & = \left \langle x , H _ { 1 } x + \cdots + H _ { n } x \right \rangle _ { T } \\
& = \left \langle x , H _ { 1 } x \right \rangle _ { T } + \cdots + \left \langle x , H _ { n } x \right \rangle _ { T } \\
& \geq \beta _ { 1 } + \cdots + \beta _ { n } \stackrel { \text {def} } { = } \beta
\end {aligned} \end {equation} $$

بنابراین، $$ H \stackrel { \text {def} } { = } ( H_ 1 + \cdots + H _ n ) $$ پسیو است.

حال (ب) را اثبات می‌کنیم. فرض کنید $$ k $$ سیستم از $$ n $$ سیستم $$ H _ i $$ اکیداً پسیو باشند ($$ 1 \le k \le n $$). فرض می‌کنیم این سیستم‌ها $$ H _ 1 $$، $$ H _ 2 $$، ... و $$ H _ k $$ نام داشته باشند. رابطه زیر را داریم:

$$ \large \begin {equation} \begin {aligned}
\langle x , H x \rangle _ { T } & = \left \langle x , H _ { 1 } x + \cdots + H _ { n } x \right \rangle _ { T } \\
& = \left \langle x , H _ { 1 } x \right \rangle _ { T } + \cdots + \left \langle x , H _ { k } x \right \rangle _ { T } + \cdots + \left \langle x , H _ { n } x \right \rangle _ { T } \\
& \geq \delta _ { 1 } \langle x , x \rangle _ { T } + \cdots + \delta _ { k } \langle x , x \rangle _ { T } + \beta _ { 1 } + \cdots + \beta _ { n } \\
& = \left ( \delta _ { 1 } + \cdots + \delta _ { k } \right ) \left\| x _ { T } \right \| x + \left ( \beta _ { 1 } + \cdots + \beta _ { n } \right )
\end {aligned} \end {equation} $$

و اثبات این بخش نیز انجام می‌شود.

برای اثبات (پ)، ضرب داخلی زیر را در نظر می‌گیریم:

$$ \large \begin {equation} \begin {aligned}
\langle u , y \rangle _ { T } & = \left \langle e + H _ { 2 } y , y \right \rangle _ { T } \\
& = \langle e , y \rangle _ { T } + \left \langle H _ { 2 } y , y \right \rangle _ { T } \\
& = \left \langle e , H _ { 1 } e \right \rangle _ { T } + \left \langle y , H _ { 2 } y \right \rangle _ { T } \geq \left ( \beta _ { 1 } + \beta _ {2 } \right )
\end {aligned} \end {equation} $$

و اثبات کامل می‌شود.

تذکر: در حالت کلی، تعداد سیستم‌های بخش‌های (الف) و (ب) قضیه ۲ را نمی‌توان نامحدود فرض کرد. اعتبار نتایج در این حالتی که سیستم‌ها نامحدود باشند، به ویژگی‌های ضرب داخلی بستگی دارد. البته، می‌توان نشان داد که اگر ضرب داخلی یک ضرب داخلی استاندارد در $$ \mathcal { L } _ 2 $$ باشد، آنگاه این تعمیم معتبر خواهد بود.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

بر اساس رای ۰ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

منابع:

Nonlinear Control Systems: Analysis and Design

سید سراج حمیدی (+)

سید سراج حمیدی دانش‌آموخته مهندسی برق است و به ریاضیات و زبان و ادبیات فارسی علاقه دارد. او آموزش‌های مهندسی برق، ریاضیات و ادبیات مجله فرادرس را می‌نویسد.