حجم کره و محاسبه آن | به زبان ساده

«کره» (Sphere) یک جسم هندسی کاملاً گرد در فضای سه‌بعدی است. این حجم هندسی را می‌توان با مجموعه‌ای از تمام نقاط واقع در فاصله $$r$$ (شعاع) از یک نقطه (مرکز) مشخص کرد. کره کاملاً متقارن است و لبه و رأس ندارد. در آموزش‌های قبلی مجله فرادرس، روش محاسبه مساحت کره را بیان کردیم. در این آموزش، با روش محاسبه حجم کره آشنا می‌شویم.

فرمول حجم کره چیست؟

فرمول حجم کره‌ای به شعاع $$r$$، برابر با $$ V=\frac43 \pi r ^ 3 $$ است.

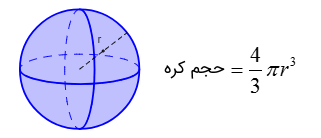
همچنین، از آموزش‌های قبل می‌دانیم که فرمول مساحت سطح کره‌ای به شعاع $$r$$ برابر با $$S= 4 \pi r ^ 2 $$ است.

جالب است بدانید که کره از بین همه اجسام هندسی با مساحت یکسان، دارای بیشترین حجم است.

اثبات فرمول حجم کره

برای اثبات فرمول حجم کره روش‌های مختلفی وجود دارد که عبارتند از: روش ارشمیدس، روش دیسک یا انتگرال‌ و روش کاوالیری. در ادامه، با استفاده از انتگرال، فرمول حجم کره را به دست خواهیم آورد.

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

شکل زیر را در نظر بگیرید.

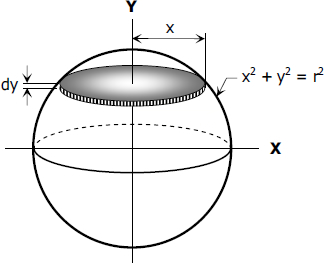
عنصر دیفرانسیلی نشان داده شده در این شکل، استوانه‌ای به شعاع $$ x $$ و ارتفاع $$dy $$ است. حجم استوانه به صورت زیر محاسبه می‌شود:

$$ \large d V = \pi x ^ 2 d y $$

مجموع عناصر استوانه‌ای از $$o$$ تا $$r$$ یک نیم‌کره است. با دو برابر کردن نیم‌کره، حجم کره به دست می‌آید:

$$ \large V = 2 \pi \int _ 0 ^ r x ^ 2 d y $$

معادله دایره $$ x ^ 2 + y ^ 2 = r ^ 2 $$ است. بنابراین، رابطه $$ x ^ 2 = r ^ 2 - y ^ 2 $$ را خواهیم داشت و می‌توانیم بنویسیم:

$$ \large \begin {align*} V & = 2 \pi \int _ 0 ^ r ( r ^ 2 - y ^ 2 ) d y = 2 \pi \left [ r ^ 2 y - \dfrac { y ^ 3 } { 3 } \right ] _ 0 ^ r \\ & = 2 \pi \left [ \left ( r ^ 3 - \dfrac { r ^ 3 } { 3 } \right ) - \left ( 0 - \dfrac { 0 ^ 3 } { 3 } \right ) \right ] \\
& = 2 \pi \left [ \dfrac { 2 r ^ 3 } { 3 } \right ] = \dfrac { 4 \pi r ^ 3 } { 3 }
\end {align*} $$

مثال های محاسبه حجم کره

در این بخش، چند مثال از محاسبه حجم کره را حل می‌کنیم.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

مثال ۱: حجم کره‌ای به شعاع $$5$$ چقدر است.

حل: طبق فرمولی که گفتیم، حجم کره برابر است با:

$$ \large V = \frac { 4 } { 3 } \pi \times 5 ^ 3 = \frac { 5 0 0 } { 3 } \pi = 1 6 6 \frac { 2 } { 3 } \pi $$

مثال ۲: اگر مساحت سطح کره‌ای برابر با $$ 144 \pi $$  باشد، حجم آن را به دست آورید.

حل: با توجه به فرمول $$4 \pi r ^ 2 $$ مربوط به مساحت سطح کره، مساحت داده شده را می‌توان به صورت زیر نوشت:

$$ \large 144 \pi = 4 \pi \times 6 ^ 2 . $$

بنابراین، می‌توان گفت که شعاع کره $$r=6$$ است. در نتیجه، حجم آن به صورت زیر به دست می‌آید:‌

$$ \large V = \frac { 4 } { 3 } \pi r ^ 3 = \frac { 4 } { 3 } \pi \times 6 ^ 3 = 2 8 8 \pi . $$

مثال ۳: یک گوی طلایی داریم که حجم آن $$ \frac { 4 \pi } { 3 } \text { cm} ^ 3 $$ است. اگر بخواهیم اندازه (شعاع) این گوی طلایی را دو برابر کنیم، به چه مقدار طلای اضافه نیاز داریم؟

حل: با توجه به فرمول $$ V = \frac { 4 } { 3 } \pi r ^ 3 $$ مربوط به حجم کره که در آن، $$ r $$ شعاع کره است، شعاع برابر با $$ r = 1 \text { cm} $$ به دست خواهد آمد. از آنجا که می‌خواهیم شعاع دو برابر، یعنی $$ 2 \text { cm} $$ شود، حجم طلای مورد نیاز برای گوی جدید، $$ \frac { 4 } { 3 } \pi \times 2 ^ 3 = \frac { 3 2 \pi }{ 3 } \left ( \text {cm} ^ 3 \right ) $$ است. در نتیجه، مقدار طلای اضافه مورد نیاز برابر خواهد بود با:

$$ \large \frac { 3 2 \pi } { 3 } \text { cm} ^ 3 - \frac { 4 \pi }{ 3 } \pi \text { cm} ^ 3 = \frac { 2 8 \pi } { 3 } \text { cm} ^ 3 . $$

مثال ۴: حجم کره $$a$$، به اندازه $$ \frac { 1 } { 2 7 } $$ برابر کوچک‌تر از کره $$ b $$ است. در این صورت، مساحت سطح کره $$a$$ چند برابر مساحت سطح کره $$ b $$ خواهد بود؟

حل: فرض کنید $$R_a$$ و $$R_b$$، به ترتیب، شعاع‌های کره‌های $$a$$ و $$b$$ باشند. با توجه به فرمول حجم $$ V = \frac { 4 } { 3 } \pi r ^ 3 $$ کره یا شعاع $$r$$، می‌توان نوشت:

$$ \large \frac { 4 } { 3 } \pi { R _ a } ^ 3 = \frac { 1 } { 2 7 } \cdot \frac { 4 } { 3 } \pi { R _ b } ^ 3 $$

که منجر به رابطه $$ R _ a = \frac { 1 } { 3 } R _ b $$ می‌شود.

بنابراین، با توجه به فرمول $$ S = 4 \pi r ^ 2 $$ مساحت سطح کره به شعاع $$r$$، مساحت سطح کره $$a$$، به اندازه $$ \left ( \frac { 1 } { 3 } \right ) ^ 2 = \frac { 1 } { 9 } $$ برابر کوچک‌تر از مساحت سطح کره $$b$$ خواهد بود.

مثال ۵: همان‌طور که در شکل زیر نشان داده شده است، می‌خواهیم یک قسمت مخروطی را از یک هندوانه کروی به شعاع $$R=5$$ جدا کنیم. این

بخش مخروطی یک کلاهک کروی به شعاع $$r=3$$ دارد. نسبت حجم کل کره اصلی به این مخروط کروی چقدر است؟

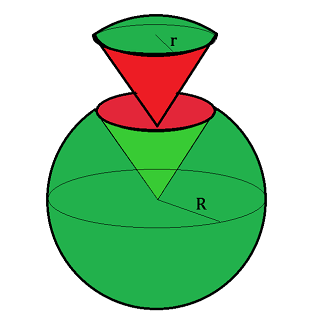
حل:‌ شکل زیر را در نظر بگیرید:

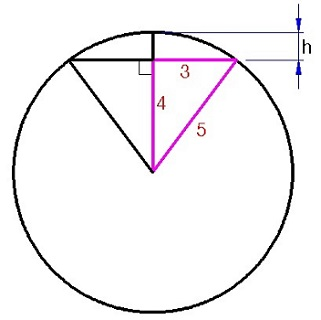
با توجه به مقادیر داده شده، یک مثلث قائم‌الزاویه با اضلاع $$3$$، $$4$$ و $$5$$ خواهیم داشت و $$h = 5-4=1$$ به دست خواهد آمد. فرمول حجم بخش کروی برابر با $$ V _ { s s } = \dfrac { 2 } { 3 } \pi R ^ 2 h $$ است و با جایگذاری مقدایر در آن، خواهیم داشت:

$$ \large V _ {ss} = \dfrac { 2 } { 3 } \pi ( 5 ^ 2 ) ( 1 ) = \dfrac { 5 0 } { 3 } \pi $$

حجم کره اصلی نیز برابر است با:

$$ \large V = \dfrac { 4 } { 3 } \pi R ^ 3 = \dfrac { 4 } { 3 } \pi ( 5 ^ 3 ) = \dfrac { 5 0 0 } { 3 } \pi $$

در نهایت، نسبت حجم کره به حجم مخروط کروی به صورت زیر محاسبه می‌شود:‌

$$ \large \dfrac { V } { V _ { s s } } = \dfrac { \dfrac { 5 0 0 } { 3 } \pi } { \dfrac { 5 0 }{ 3 } \pi } = \dfrac { 5 0 0 } { 5 0 } = 10 $$

مثال ۶: حجم کره شکل زیر را به دست آورید (مقدار $$\pi$$ را برابر با $$3.14$$ در نظر بگیرید).

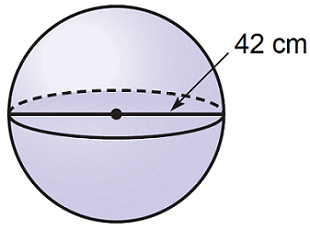
حل: قطر کره برابر با $$42\, \text{cm}$$ است و بنابراین، شعاع آن $$r = 21\, \text{cm}$$ خواهد بود. با کمک فرمول حجم کره، خواهیم داشت:

$$ \large V = \frac 43 \pi r ^ 3 = \frac 43 \times 3.14 \times 21^ 3 =\frac 43 \times 3.14 \times 9261 =38,772.7\; \text{cm}^3 $$