تابع مولد — از صفر تا صد
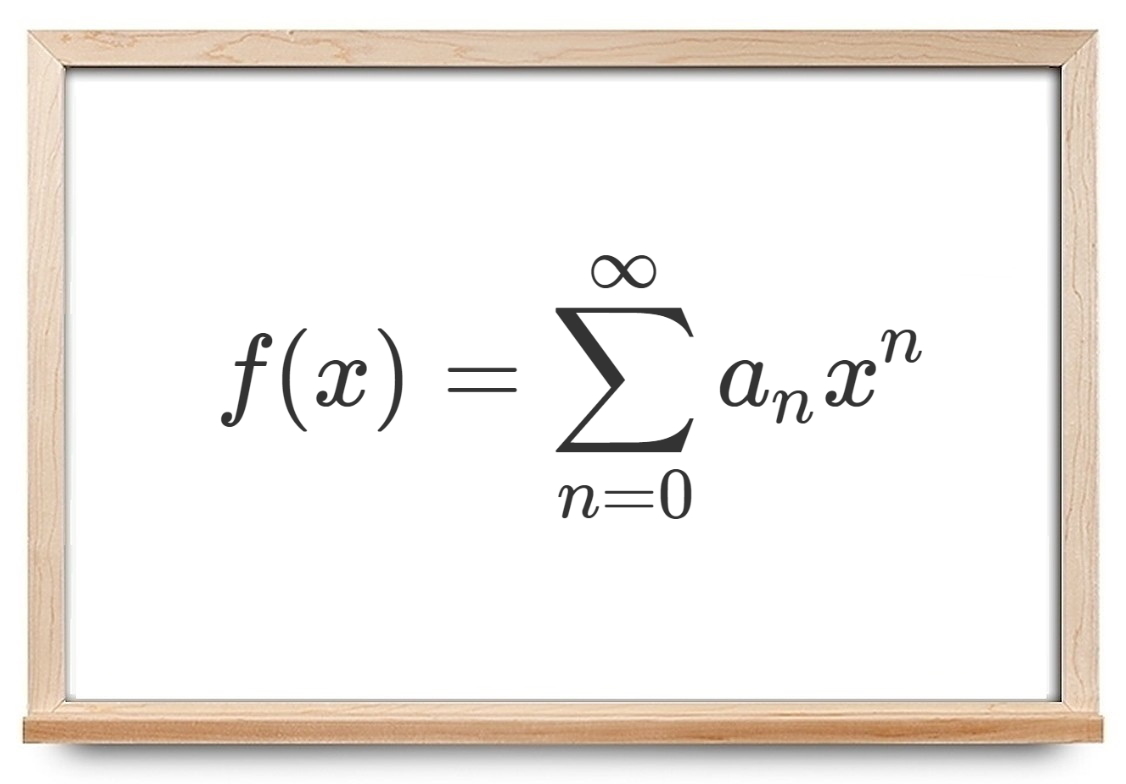
«تابع مولد» (Generating Function) یک چندجملهای است که ضرایب آن متناظر با دنبالهای از اعداد هستند. با توجه توانایی توابع مولد در رمزبندی اطلاعات در یک دنباله از اعداد صحیح، این توابع ابزار قدرتمندی هستند که میتوان از آنها در روابط بازگشتی استفاده کرد. روشهایی مانند کسرهای جزئی، ضرب چندجملهایها و مشتقات به حل روابط بازگشتی کمک میکنند.
تابع مولد معمولی
یک «تابع مولد معمولی» (Ordinary Generating Function) به فرم $$ f ( x ) = \displaystyle \sum _ { n = 0 } ^ { \infty } a _ n x ^ n $$ نوشته میشود که در حل مسائل مختلف کاربرد دارد.
مثال اول تابع مولد معمولی
به چند روش میتوان اعدادی را نوشت که مجموع آنها برابر با ۱۰ باشد، به طوری که دقیقاً یکی از عناصر دو مجموعه $$ \{ 2 , 3 , 6 , 7 \}$$ و $$ \{ 3 , 4 , 5 , 8 \}$$ را داشته باشد؟
حل: دو چندجملهای $$ x ^ 2 + x ^ 3 + x ^ 6 + x ^ 7 $$ و $$ x ^ 3 + x ^ 4 + x ^ 5 + x ^ 8 $$ را در نظر بگیرید. در چندجملهای نخست، ضریب $$ x ^ n $$ عددی است که با استفاده از یک عنصر از مجموعه اول جمع $$n$$ را میسازد. همین گفته برای چندجملهای دوم نیز برقرار است. برای مثال، ضریب $$ x ^ 4 $$ در چندجملهای دوم برابر با ۱ است و یک راه برای تشکیل مجموع ۴ با استفاده از فقط یک عنصر از مجموعه دوم وجود دارد.
اکنون ضرب چندجملهایها را در نظر بگیرید:
$$ \large \big ( x ^ 2 + x ^ 3 + x ^ 6 + x ^ 7 \big ) \big ( x ^ 3 + x ^ 4 + x ^ 5 + x ^ 8 \big ) . $$
میخواهیم بدانیم که ضریب $$ x ^ n $$ در ضرب چندجملهایها چه مفهومی دارد. این ضریب تعداد راههایی را نشان میدهد که میتوان مجموع $$n$$ را با استفاده از دقیقاً یک عنصر از هر مجموعه تشکیل داد. حاصلضرب به صورت زیر است:
$$ \large \begin {aligned} & \big ( x ^ 2 + x ^ 3 + x ^ 6 + x ^ 7 \big ) \big ( x ^ 3 + x ^ 4 + x ^ 5 + x ^ 8 \big ) \\ & = x ^ 5 + 2 x ^ 6 + 2 x ^ 7 + x ^ 8 + x ^ 9 + 3 x ^ { 1 0 } + 3 x ^ { 1 1 } + x ^ { 1 2 } + x ^ { 1 4 } + x ^ { 1 5 } . \end {aligned} $$
لازم به ذکر است که ضریب $$ x ^ n $$ برای $$ n >15$$ برابر با $$0$$ است، زیرا نمیتوانیم مجموعی را بزرگتر از $$15$$ با استفاده از یکی از مجموعهها بسازیم. همین گفته برای $$ n < 5 $$ نیز صادق است.
وقتی $$ n = 10 $$ باشد، ضریب $$3$$ است. این بدین معنی است که ۳ راه برای ساختن $$10$$ وجود دارد. اگر ضرب را به طور کامل با فرمول توزیعی گسترش دهیم، خواهیم دید که سه تا $$ x ^{ 10}$$ از ضرب $$ x ^2$$ در $$ x^8 $$، ضرب $$ x ^ 6 $$ در $$ x ^ 4 $$ و ضرب $$ x ^ 7 $$ در $$ x ^ 3 $$ وجود دارد.
ایده معنی دادن به ضریب $$ x ^ n $$ بدون معنی دادن به $$ x $$ در حقیقت ایده تابع مولد است. یک تابع مولد تعداد اشیا را با استفاده از سریهای توانی رسمی که چندجملهای با احتمالاً بینهایت جمله (توانهای صحیح) است، رمزگذاری میکند. توجه کنید که اصطلاح رسمی به این دلیل استفاده میشود که یک مفهوم جبری است، نه یک مفهوم تحلیلی.
در مثال بالا، ما میتوانستیم به سادگی تعداد روشهای تشکیل $$10$$ را با بررسی محاسبه کنیم. با این حال، اگر توابع چندجملهای به شکل فشردهتری (مانند استفاده از مجموع سری هندسی) بیان شود، توابع مولد بسیار مفیدتر هستند و سپس ضرب ممکن است حذف و محاسبه آسانتر شود.
مثال دوم تابع مولد معمولی
تابع مولد مربوط به ارزش ظاهری وجه ۱ و همچنین تابع مولد مجموع مقادیر ظاهری وجه ۲ یک تاس را بیابید.
حل: برای یک تاس ششوجهی استاندارد، دقیقاً یک راه برای برای آمدن هر عدد از ۱ تا ۶ است. بنابراین، میتوانیم آن را با سری توانی $$ R _ 1 ( x ) = x ^ 1 + x ^ 2 + x ^ 3 + x ^ 4 + x ^ 5 + x ^ 6 $$ رمزگذاری کنیم. نماها عددی را که پس از انداختن تاس میآید نشان میدهند و ضرایب تعداد راههایی است که مقدار میتواند به آن تخصیص یابد.
برای ۲ تاس، میتوانیم به همین ترتیب مقادیر احتمالی را فهرست کرده و بنویسیم:
$$ \large R _ 2 ( x ) = x ^ 2 + 2 x ^ 3 + 3 x ^ 4 + 4 x ^ 5 + 5 x ^ 6 + 6 x ^ 7 + 5 x ^ 8 + 4 x ^ 9 + 3 x ^ { 1 0 } + 2 x ^ { 1 1 } + x ^ { 1 2 } . $$
یک راه سرراستتر، استفاده از $$ R _ 2 ( x ) = [ R _ 1 ( x ) ] ^ 2 $$ است، بنابراین، میتوانیم بدون شمارش هر جمله، آن را محاسبه کنیم.
مثال سوم تابع مولد معمولی
چه تعداد جواب صحیح نامنفی در معادله $$ a + b + c = 20 $$ صدق میکند؟
حل: ابتدا مسئله عمومیتر یافتن تعداد جوابهای صحیح نامنفی معادله $$ a + b + c = n $$ را در نظر میگیریم. از آنجا که مقدار $$ a $$ میتواند هر عدد صحیح نامنفی $$ 0$$، $$ 1 $$، $$ 2 $$، $$\cdots$$، $$i$$ و ... باشد، میتوانیم آن را با یک تابع مولد نشان دهیم:
$$ \large A ( x ) = 1 + x + x ^ 2 + \cdots + x ^ i + \cdots . $$
تابع مولد مشابهی برای مقادیر ممکن $$ b $$ و $$ c $$ داریم. بنابراین، تابع مولد برای تعداد جوابها $$ A ( x ) \times B ( x ) \times C ( x ) = [ A ( x ) ] ^ 3 $$ است. با این حال، یافتن این ضرب میتواند بسیار خستهکننده باشد.
برای رفع این مسئله، $$ A( x ) $$ به به کسر گویای $$ \frac { 1 } { 1 - x }$$ تبدیل میکنیم که از مجموع یک تصاعد هندسی به دست آمده است. بنابراین، $$ [ A ( x ) ] ^ 3 = \frac { 1 } { ( 1 - x ) ^ 3 } $$ را بررسی میکنیم. این عبارت را میتوان با استفاده از قضیه دوجملهای منفی بسط داد:
$$ \large \frac { 1 } { ( 1 - x ) ^ 3 } = { 2 \choose 2 } + { 3 \choose 2 } x + { 4 \choose 2 } x ^ 2 + \cdots + { i + 2 \choose 2 } x ^ i + \cdots . $$
بنابراین، وقتی $$ n = 20 $$ باشد، عبارت $$ { 2 2 \choose 2 } $$ را خواهیم داشت.
حل رابطه بازگشتی همگن
در حالت کلی، یک رابطه بازگشتی برای اعداد $$ \{ c _ i \} _ { i = 1 } ^ { \infty } $$ راهی برای بیان $$ c _ n$$ برحسب $$k$$ جمله قبلی دنباله، به ازای تعدادی عدد صحیح مثبت $$k$$ است. یک رابطه بازگشتی خطی همگن رابطهای به فرم $$ c _ n + q _ 1 c _ { n - 1 } + q _ 2 c _ { n - 2 } + \cdots +q_ k c _ { n - k } = 0 $$ است. این رابطه خطی است، زیرا هر جمله آن فقط یک تکجملهای به فرم $$ c _ i $$ است و همگن است، زیرا سمت راست آن برابر با ۰ است.
اگر سمت راست این رابطه تابعی غیرصفر از $$ n $$ باشد، آنگاه معادله ناهمگن نامیده میشود. برای حل کامل یک رابطه بازگشتی، به مقادیر اولیه $$k$$ جمله ابتدایی نیاز داریم.
مثال رابطه بازگشتی همگن
مقدار صریح $$ c _ n $$ را بیابید، در صورتی که داشته باشیم:
$$ \large c _ n - 3 c _ { n - 2 } - 2 c _ { n - 3 } = 0 , \mbox{ } n \geq 3 $$
که برای آن، $$ c _ 2 = 12 $$، $$ c _ 1 = 5 $$ و $$ c _ 0 = 5 $$.
حل: تابع مولد زیر را در نظر بگیرید:
$$ \large c ( x ) = c _ 0 + c _ 1 x + c _ 2 x ^ 2 + c _ 3 x ^ 3 + \cdots . $$
از آنجا که رابطه $$ c _ n - 3 c _ { n - 2 } - 2 c _ { n - 3 } = 0 $$ را داریم، تابع $$ 2 x ^ 3 c ( x ) + 3 x ^ 2 c ( x ) - c ( x ) $$ را در نظر میگیریم:
$$ \large \begin {array} { r l l l r l l l l l } 2 x ^ 3 c ( x ) & = & & & & + 2 c _ 0 x ^ 3 & + 2 c _ 1 x ^ 4 & + \cdots \\ + 3 x ^ 2 c ( x ) & = & & & 3 c _ 0 x ^ 2 & + 3 c _ 1 x ^ 3 & + 3 c _ 2 x ^ 4 & + \cdots \\ - c ( x ) & = & - c _ 0 & - c _ 1 x & - c _ 2 x ^ 2 & - c _ 3 x ^ 3 & - c _ 4 x ^ 4 & - \cdots \\ \hline & = & - c _ 0 & - c _ 1 x & + ( 3 c _ 0 - c _ 2 ) x ^ 2 & + 0 & + 0 & + 0 \ldots \\ & = & -5 & -5 x & + 3 x ^ 2 . & & & \\ \end {array} $$
بنابراین، $$ \big ( 2 x ^ 3 + 3 x ^ 2 - 1 \big ) c ( x ) = - 5 - 5 x + 3 x ^ 2 $$ را به دست خواهیم آورد و خواهیم داشت:
$$ \large c ( x ) = \frac { - 5 - 5 x + 3 x ^ 2 } { 2 x ^ 3 + 3 x ^ 2 - 1 } = - \frac { 3 } { 2 x - 1 } + \frac { 3 } { x + 1 } - \frac { 1 } { ( x + 1 ) ^ 2 } . $$
در نتیجه، با استفاده از قضیه دوجملهای منفی یا سری تیلور، میتوانیم هریک از جملات را بسط دهیم که نتیجه آن به صورت زیر است:
$$ \large c ( x ) = \sum _ { n = 0 } ^ { \infty } \big [ 3 \times 2 ^ n - ( - 1 ) ^ n ( n - 2 ) \big ] x ^ n . $$
بنابراین، $$ c _ n = 3 \times 2 ^ n - ( - 1 ) ^ n ( n - 2 ) $$.
اکنون مثال بالا را عمومیت میدهیم. دنباله اعداد $$ c _ 0$$، $$ c _ 1$$، $$ c _ 2 $$ و... را در نظر بگیرید که در رابطه بازگشتی $$ c _ k + q _ 1 c _ { k - 1 } + q _ 2 c _ { k - 2 } + \cdots + q _ d c _ { k - d } = 0 . $$ صدق میکنند. در نتیجه، جملات رابطه بازگشتی، ضرایب یک تابع مولد با تابع گویای $$ f ( x ) = p ( x ) / q ( x ) $$ هستند. به طور خاص، داریم:
$$ \large f ( x ) = \sum \limits _ { k = 0 } ^ { \infty } c _ k x ^ k = \frac { m _ 0 + m _ 1 x + m _ 2 x ^ 2 + \cdots + m _ j }{ 1 + q _ 1 x + q _ 2 x ^ 2 + \cdots + q _ d x ^ d } $$
که $$ j + 1 $$ جمله اولیه $$ c _ 0 $$، $$ c _ 1$$، ... و $$ c _ k $$ و $$ m _ i $$ها به صورت زیر تعریف میشوند:
$$ \large \begin {array} {l} m _ 0 = c _ 0 \\ m _ 1 = c _ 1 + q _ 1 c _ 0 \\ m _ 2 = c _ 2 + q _ 1 c _ 1 + q _ 2 c _ 0 . \end {array} $$
میتوانیم از این برای حل صریح $$ c _ k $$ با یافتن ریشههای مخرج و استفاده از تجزیه به کسر جزئی تابع گویا استفاده کنیم. با استفاده از قضیه دوجملهای منفی برای هر جمله، میتوانیم ضریب $$ c _ k $$ را حل کنیم. قضیه زیر، این موضوع را بیان میکند.
قضیه
برای یک رابطه بازگشتی به فرمی که در بالا توصیف شد، چندجملهای مشخصه بازگشتی به صورت زیر است:
$$ \large x ^ k + q _ 1 x ^ { k - 1 } + \cdots + q _ { x - 1 } x + q _ k . $$
فرض کنید چندجملهای مشخصه دارای ریشههای $$ \alpha _ i $$ با تکرار $$ m _ i $$ برای $$ i = 1 , , \ldots , j $$ است. در نتیجه، جواب عمومی رابطه بازگشتی به صورت زیر خواهد بود:
$$ c _ n = \left ( a _ { 1 , 1 } + a _ { 1 , 2 } n + \cdots + a _ { 1 , m _ 1 } n ^ { m _ 1 - 1 } \right ) \alpha _ 1 ^ n + \cdots + \left ( a _ { j , 1 } + a _ { j , 2 } n + \cdots + a _ { j , m _ j } n ^ { m _ j - 1 } \right ) \alpha _ j ^ n . $$
ثابتهای $$a _ { 1 , 1 }$$، $$a _ {1,2}$$، ... و $$ a _ {j,m_j}$$ به گونهای انتخاب میشوند که در شراط اولیه صدق کنند. دقت کنید که تعداد این ثابتها $$ k $$ است و به همین دلیل است که به $$k $$ مقدار اولیه نیاز داریم.
حل رابطه بازگشتی خطی ناهمگن
با تغییر $$0$$ به $$n$$ در سمت راست رابطه بازگشتی همگن، یک رابطه بازگشتی ناهمگن خواهیم داشت که به صورت زیر است:
$$ \large c _ n + q _ 1 c _ { n - 1 } + q _ 2 c _ { n - 2 } + \cdots + q _ k c _ { n - k } = f ( n ) . $$
حتی با تغییرات کوچک، جوابها بسیار پیچیده خواهند شد.
مثال اول رابطه بازگشتی ناهمگن
مقدار $$ c _ n $$ رابطه زیر را پیدا کنید:
$$ \large c _ n - 3 c _ { n - 2 } - 2 c _ { n - 3 } = 4 n - 2 , \mbox { } n \geq 3 $$
که برای آن، $$ c _ 2 = 12 $$، $$ c _ 1 = 5 $$ و $$ c _ 0 = 5 $$.
حل: تابع مولد زیر را در نظر بگیرید:
$$ \large c ( x ) = c _ 0 + c _ 1 x + c _ 2 x ^ 2 + c _ 3 x ^ 3 + \cdots . $$
از آنجا که $$ c _ n - 3 c _ { n - 2 } - 2 c _ { n - 3 } = 4 n - 2 $$، تابع $$ 2 x ^ 3 c ( x ) + 3 x ^ 2 c ( x ) - c ( x ) $$ را در نظر بگیرید:
$$ \large \begin {array} { r l l l r l l l l l } 2 x ^ 3 c ( x ) & = & & & & + 2 c _ 0 x ^ 3 & + 2 c _ 1 x ^ 4 & + & \cdots \\ + 3 x ^ 2 c ( x ) & = & & & 3 c _ 0 x ^ 2 & + 3 c _ 1 x ^ 3 & + 3 c _ 2 x ^ 4 & + & \cdots \\ - c ( x ) & = & - c _ 0 & - c _ 1 x & - c _ 2 x ^ 2 & - c _ 3 x ^ 3 & - c _ 4 x ^ 4 & - & \cdots \\ \hline & = & - 5 & -5 x & +3 x ^ 2 & - 10 x ^ 3 & - 14 x ^ 4 & - & \cdots \\ \end {array} $$
بنابراین، با استفاده از قضیه دوجملهای منفی یا سری تیلور، میتوانیم هرکدام از این جملات را بسط دهیم و در نتیجه، بنویسیم:
$$ c _ n = \frac { 1 0 1 } { 1 8 } \times ( - 1 ) ^ n + \frac { 6 5 } { 9 } \times 2 ^ n - \frac { 1 } { 3 } \times ( n + 1 ) \times ( - 1 ) ^ n - \frac { 5 } { 2 } \times 1 ^ n - 1 \times ( n + 1 ) \times ( 1 ) ^ n . $$
از آنجا که ما صرفاً با یک ساختار نظری سر و کار داریم، میتوانیم بسیاری از عملیات تابع را برای توابع مولدی که ایجاد کردهایم، اعمال کنیم. به عنوان مثال، میتوانیم آنها را در هم ضرب کنیم یا حتی از آنها مشتق با انتگرال بگیریم.
مثال دوم رابطه بازگشتی ناهمگن
فرم بسته عبارت زیر را بیابید:
$$ \large c _ n = \sum _ { i = 0 } ^ n ( 2 + i ) 2 ^ { n - i } . $$
حل: این مثال به اندازه کافی ساده است به گونهای که میتوانیم به آسانی به جواب برسیم. با این حال، برای درک آنچه درباره تابع مولد گفتیم، این مثال را با استفاده از توابع مولد حل میکنیم.
تابع زیر را تعریف میکنیم:
$$ \large c ( x ) = c _ 0 + c _ 1 x + c _ 2 x ^ 2 + c _ 3 x ^ 3 + \cdots . $$
ابتدا، $$ c _ n $$ را میتوانیم به فرم $$ \sum a _ i \times b _ { n - i } $$ بنویسیم یک کانولوشن است. این منجر به تعریف چندجملهای زیر میشود:
$$ \large \begin {aligned} a ( x ) & = 2 + 3 x + 4 x ^ 2 + \cdots + ( 2 + i ) x ^ i + \cdots \\ & = \frac { 1 } { 1 - x } + \frac { 1 } { ( 1 - x ) ^ 2 } = \frac { 2 - x } { ( 1 - x ) ^ 2 } , \\\\ b ( x ) & = 2 ^ 0 + 2 ^ 1 x + 2 ^ 2 x + \cdots + 2 ^ i x ^ 2 + \cdots \\ & = \frac { 1 } { 1 - 2 x } . \end {aligned} $$
بنابراین، $$ c ( x ) = a ( x ) \times b ( x ) $$ را داریم. با استفاده از توابع بازگشتی، میتوان نوشت:
$$ \large \begin {aligned} c ( x ) & = a ( x ) \times b ( x ) \\ & = \frac { 2 - x } { ( 1 - x ) ^ 2 } \times \frac { 1 } { 1 - 2 x } \\ & = - \frac { 3 } { 1 - x } - \frac { 1 } { ( 1 - x ) ^ 2 } + \frac { 6 } { 1 - 2 x } . \end {aligned} $$
بنابراین، $$ c _ n = - 3 - ( n + 1 ) + 6 \times 2 ^ n = 6 \times 2 ^ n - n - 4 $$.
افزایش و کاهش نمای توابع مولد
وقتی تابع مولدی برای یک مسئله مشخص داشته باشیم، میتوانیم آن را برای حل مسائل ترکیبی دیگر به کار ببریم.
تعریف
برای تابع مولد $$ f ( x ) = a _ 0 + a _ 1 x + a _ 2 x ^ 2 + \cdots $$، میتوانیم با ضرب $$ x ^ m $$ در آن، ضرایب را $$m$$ تا به راست جابهجا کنیم:
$$ \large x ^ m f ( x ) = a _ 0 x ^ m + a _ 1 x ^ { m + 1 } + a _ 2 x ^ { m + 2 } + \cdots . $$
مثال افزایش و کاهش نمای توابع مولد
اگر دقیقاً یک عضو از $$ \{ 2 , 3 , 4 , \dots \} $$ انتخاب کنیم، چه تعداد راه برای انتخاب یک عدد مشخص وجود دارد؟ جواب را برحسب تابع مولد ساده شده بنویسید.
حل: مشابه مثالی که در ابتدای آموزش بیان کردیم، یک تابع مولد داریم که هر جمله $$ x ^ n $$ برای هر مقدار $$ n $$ در مجموعه دارای یک ضریب ۱ است:
$$ \large x ^ 2 + x ^ 3 + x ^ 4 + \cdots . $$
این تابع مولد مشابه تابع مولد ابتدای متن است، با این تفاوت که ضرایب آن دو بار به راست جابهجا شدهاند. با استفاده از این، میتوان تابع مولد را به فرم خلاصه شده زیر بیان کنیم:
$$ \large x ^ 2 \times \frac { 1 } { 1 - x } = \frac { x ^ 2 } { 1 - x } . $$
مقیاس بندی نمای تابع مولد
در این بخش، درباره تغییر مقیاس نمای تابع مولد بحث میکنیم.
تعریف
تابع مولد $$ f ( x ) = a _ 0 + a _ 1 x + a _ 2 x ^ 2 + \cdots $$ را در نظر بگیرید. میتوانیم نمای آن را با ترکیب آن با تابع $$ g ( x ) = x ^ m $$ به اندازه $$m$$ برابر کنیم:
$$ \large f ( x ^ m ) = a _ 0 + a _ 1 x ^ { m } + a _ 2 x ^ { 2 m } + \cdots . $$
مثال تغییر مقیاس نمای تابع مولد
اگر دقیقاً یکی از اعضای مجموعه اعداد زوج $$ \{ 0 , 2 , 4 , \dots \} $$ را انتخاب کنیم، چند راه برای انتخاب یک عدد مشخص وجود دارد؟ جواب را برحسب تابع مولد ساده شده بنویسید.
حل: یک تابع مولد خواهیم داشت که هر جمله $$ x ^ n $$ آن برای هر مقدار زوج $$n$$ دارای ضریب ۱ خواهد بود:
$$ \large 1 + x ^ 2 + x ^ 4 + \cdots . $$
این تابع مشابه تابع مولد ابتدای متن است، با این تفاوت که هر نمای آن دو برابر شده است. با استفاده از روش تغییر مقیاس، میتوانیم با استفاده از $$ \phi ( x ^ 2 ) $$ یک عبارت سادهتر برای تابع مولد بیان کنیم:
$$ \large \phi ( x ^ 2 ) = \frac { 1 } { 1 - x ^ 2 } . $$
توابع مولد دنبالههای رایج
توابع مولد مربوط به دنبالههای رایج در جدول زیر آورده شدهاند.
| دنباله | تابع مولد |
| $$ 1 , \, 1 , \, 1 , \, 1 , \, \ldots , \, 1 , \, \ldots $$ | $$ { 1 \over 1 - z } = \sum _ { N \ge 0 } z ^ N $$ |
| $$ 0 , \, 1 , \, 2 , \, 3 , \, 4 , \, \ldots , \, N , \, \ldots $$ | $$ { z \over ( 1 - z ) ^ 2 } = \sum _ { N \ge 1 } N z ^ N $$ |
| $$ 0 , \, 0 , \, 1 , \, 3 , \, 6 , \, 1 0 , \, \ldots , \,{ N \choose 2 } , \, \ldots $$ | $$ { z ^ 2 \over ( 1 - z ) ^ 3 } = \sum _ { N \ge 2 } { N \choose 2 } z ^ N $$ |
| $$ 0 , \, \ldots , \, 0 , \, 1 , \, M + 1 , \, \ldots , \, { N \choose M } , \, \ldots $$ | $$ { z ^ M \over ( 1 - z ) ^ { M + 1 } } = \sum _ { N \ge M }{ N \choose M } z ^ N $$ |
| $$ 1 , \, M , \, { M \choose 2 } \, \ldots , \, { M \choose N } , \, \ldots , \, M , \, 1 $$ | $$ { ( 1 + z ) ^ M } = \sum _ { N \ge 0 } { M \choose N } z ^ N $$ |
| $$ 1 , \, M + 1 , \, { M + 2 \choose 2 } , \, { M + 3 \choose 3 } ,\, \ldots $$ | $$ { 1 \over ( 1 - z ) ^ { M + 1 } } = \sum _ { N \ge 0 }{ N + M \choose N } z ^ N $$ |
| $$ 1 , \, 0 , \, 1 , \, 0 , \, \ldots , \, 1 , \, 0 , \, \ldots $$ | $$ { 1 \over 1 - z ^ 2 } = \sum _ { N \ge 0 } z ^ { 2 N } $$ |
| $$ 1 , \, c , \, c ^ 2 , \, c ^ 3 , \, \ldots, \, c ^ N , \, \ldots $$ | $$ { 1 \over 1 - c z } = \sum _ { N \ge 0 } c ^ N z ^ N $$ |
| $$ 1 , \, 1 , \, { 1 \over 2 ! } , \, { 1 \over 3 ! } , \,{ 1 \over 4 ! } , \, \ldots , \, { 1 \over N ! } , \, \ldots $$ | $$ e ^ z = \sum _ { N \ge 0 } { \displaystyle z ^ N \over N ! } $$ |
| $$ 0 , \, 1 , \, { 1 \over 2 } , \, { 1 \over 3 } , \,{ 1 \over 4 } , \, \ldots , \, { 1 \over N } , \, \ldots $$ | $$ \ln { 1 \over 1 - z } = \sum _ { N \ge 1 } { \displaystyle z ^ N \over N } $$ |
| $$ 0 , \, 1 , \, 1 + { 1 \over 2 } , \, 1 + { 1 \over 2 } +{ 1 \over 3 } , \, \ldots , \, H _ N , \, \ldots $$ | $$ { 1 \over 1 - z } \ln { 1 \over 1 - z } = \sum _ { N \ge 1 } H _ N z ^ N $$ |
| $$ 0 , \, 0 , \, 1 , \, 3 ( { 1 \over 2 } + { 1 \over 3 } ) , \, 4 ( { 1 \over 2 } + { 1 \over 3 } + { 1 \over 4 } ) , \, \ldots $$ | $$ { z \over ( 1 - z ) ^ 2 } \ln { 1 \over 1 -z } = \sum _ { N \ge 0 } N ( H_ N - 1 ) z ^ N $$ |
عملیات روی توابع مولد
فرض کنید توابع مولد $$ A(z)=\sum_{k\ge0}a_kz^k $$ و $$B(z)=\sum_{k\ge0}b_kz^k $$، به ترتیب، مربوط به دنبالههای $$a_0,a_1,\ldots,a_k,\ldots$$ و $$b_0,b_1,\ldots,b_k,\ldots$$ باشند. مهمترین عملیات روی توابع مولد در جدول زیر ارائه شده است.
| عملیات | نتیجه |
| جابهجایی به راست | $$ z A ( z ) = \sum _ { n \ge 1 } a _ { n - 1 } z ^ n $$ |
| جابهجایی به چپ | $$ { A ( z ) - a _ 0 \over z } = \sum _ { n \ge 0 } a _ { n+ 1 } z ^ n $$ |
| ضرب اندیس (مشتقگیری) | $$ A ^ \prime ( z ) = \sum _ { n \ge 0 } ( n + 1 ) a _ { n + 1 } z ^ n $$ |
| تقسیم اندیس (انتگرالگیری) | $$ \int _ 0 ^ z A ( t ) d t = \sum _ { n \ge 1 } { a _ { n - 1 } \over n } z ^ n $$ |
| مقیاسبندی | $$ A ( \lambda z ) = \sum _ { n \ge 0 } \lambda ^ n a _ n z ^ n $$ |
| جمع | $$ A ( z ) + B ( z ) = \sum _ { n \ge 0 } ( a _ n + b _ n ) z ^ n $$ |
| تفریق | $$ { ( 1 - z ) A ( z ) } = a _ 0 + \sum _ { n \ge 1 } ( a _ n - a _ { n - 1 } ) z ^ n $$ |
| کانولوشن | $$ { A ( z ) B ( z ) } =\sum _ { n \ge 0 } \Bigl ( \, \sum _ { 0 \le k \le n } a _ k b _ { n - k } \Bigr ) z ^ n $$ |
| جمع جزئی | $$ { A ( z ) \over 1 - z } = \sum _ { n \ge 0 } \Bigl ( \, \sum _{ 0 \le k \le n } a _ k \Bigr ) z ^ n $$ |
توابع مولد نمایی
دنبالههایی وجود دارند که تابع مولد مربوط به آنها نمایی است. این دنبالهها و تابع مولد مربوط به آنها در جدول زیر ارائه شده است.
| دنباله | تابع مولد نمایی |
| $$ 1 , \, 1 , \, 1 , \, 1 , \, \ldots , \, 1 , \, \ldots $$ | $$ e ^ z = \sum _ { N \ge 0 } { z ^ N \over N ! } $$ |
| $$ 0 , \, 1 , \, 2 , \, 3 , \, 4 , \, \ldots , \, N , \, \ldots $$ | $$ z e ^ z = \sum _ { N \ge 1 } { z ^ N \over ( N - 1 ) ! } $$ |
| $$ 0 , \, 0 , \, 1 , \, 3 , \, 6 , \, 1 0 , \, \ldots , \, { N \choose 2 } , \, \ldots $$ | $$ { 1 \over 2 } z ^ 2 e ^ z = { 1 \over 2 } \sum _ { N \ge 2 }{ z ^ N \over ( N - 2 ) ! } $$ |
| $$ 0 , \, \ldots , \, 0 , \, 1 , \, M + 1 , \, \ldots , \,{ N \choose M } , \, \ldots \qquad $$ | $$ { 1 \over M ! } z ^ M e ^ z = { 1 \over M ! } \sum _ { N \ge M } { z ^ N \over ( N - M ) ! } $$ |
| $$ 1 , \, 0 , \, 1 , \, 0 , \, \ldots , \, 1 , \, 0 , \, \ldots $$ | $$ { 1 \over 2 } ( e ^ z + e ^ { - z } ) = \sum _ { N \ge 0 } { 1 + ( - 1 ) ^ N \over 2 } { z ^ { N } \over N ! } \qquad $$ |
| $$ 1 , \, c , \, c ^ 2 , \, c ^ 3 , \, \ldots , \, c ^ N , \, \ldots $$ | $$ e ^ { c z } = \sum _ { N \ge 0 } { c ^ N z ^ N \over N ! } $$ |
| $$ 0 , \, 1 , \, { 1 \over 2 } , \, { 1 \over 3 } , \, \ldots , \,{ 1 \over N + 1 } , \, \ldots $$ | $$ { \displaystyle e ^ z - 1 \over z } = \sum _ { N \ge 0 }{ \displaystyle z ^ N \over ( N + 1 ) ! } $$ |
| $$ 1 , \, 2 , \, 6 , \, 2 4 , \, \ldots , \, N ! , \, \ldots $$ | $$ { \displaystyle 1 \over 1 - z } = \sum _ { N \ge 0 } { \displaystyle N ! z ^ N \over N ! } $$ |
همانند توابع مولد معمولی، استفاده از عملیات ساده بر روی این توابع نمایی امکانپذیر است. این عملیات در جدول زیر آورده شدهاند.
| عملیات | نتیجه |
| جابهجایی راست (انتگرالگیری) | $$ \int _ 0 ^ z A ( t ) d t = \sum _ { n \ge 1 } a _ { n - 1 }{ z ^ n \over n ! } $$ |
| جابهجابب چپ (مشتقگیری) | $$ A ^ \prime ( z ) = \sum _ { n \ge 0 } a _ { n + 1 } { z ^ n \over n ! } $$ |
| ضرب اندیس | $$ z A ( z ) = \sum _ { n \ge 0 } n a _ { n - 1 } { z ^ n \over n ! } $$ |
| تقسیم اندیس | $$ ( A ( z) - A ( 0 ) ) / z = \sum _ { n \ge 1 } { a _ { n + 1 } \over n + 1 } { z ^ n \over n ! } $$ |
| جمع | $$ A ( z ) + B ( z ) = \sum _ { n \ge 0 } ( a_ n + b _ n ){ z ^ n \over n ! } $$ |
| تفریق | $$ A ^ \prime ( z ) - A ( z ) = \sum _ { n \ge 0 } ( a _ { n + 1 } - a _ n ) { z ^ n \over n ! } $$ |
| کانولوشن دوجملهای | $$ { A ( z ) B ( z ) } = \sum _ { n \ge 0 } \biggl ( \> \sum _ { 0 \le k \le n } { n \choose k } a _ k b _ { n - k } \biggr ){ z ^ n \over n ! } \qquad $$ |
| جمع دوجملهای | $$ e ^ z A ( z ) = \sum _ { n \ge 0 } \biggl ( \> \sum _ { 0 \le k \le n } { n \choose k } a _ k \biggr ) { z ^ n \over n ! } $$ |










