انواع سیستم ها در پردازش سیگنال— به زبان ساده
در آموزشهای پیشین مجله فرادرس، با انواع سیگنالها آشنا شدیم. در این آموزش، درباره انواع سیستم ها بحث خواهیم کرد.
سیستم چیست؟
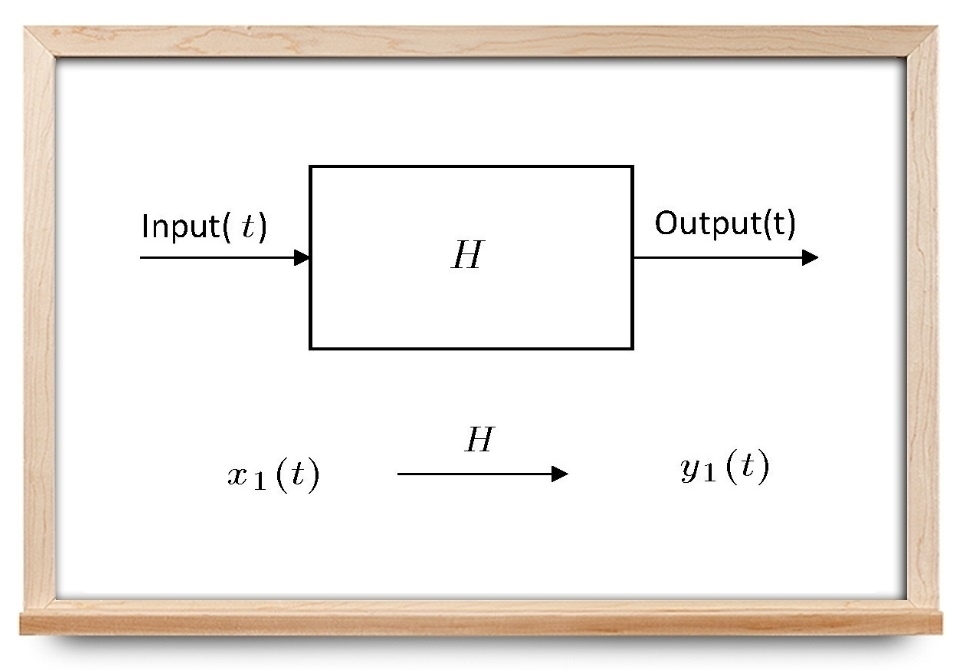
به طور خلاصه میتوان گفت که سامانه یا سیستم مجموعهای از اجزا است که یک ورودی را میگیرد و یک خروجی را نتیجه خواهد دارد.
سیستمها انواع مختلفی دارند و به روشهای مختلف میتوان آنها را کنترل کرد. این انواع، کاربردهای مهمی در زمینه سیستمها دارند.
نمایش سیستمها
سه روش عمومی برای نمایش سیستمها وجود دارد:
- معادلات تفاضلی
- نمودارهای بلوکی
- معادلههای عملگر
معادلات تفاضلی روشهای ریاضی نمایش سیستمها و اغلب به صورت بازگشتی هستند؛ به عنوان مثال، دنباله فیبوناچی. در هر گام از این دنباله، دو ورودی قبلی با هم جمع میشوند. بنابراین، اگر $$ x [n] $$ به عنوان ورودی فعلی و $$y [ n]$$ خروجی باشند، خواهیم داشت:
$$ \large y [ n ] = y [ n - 1 ] + y [ n - 2 ] + x [ n ] $$
که دنباله فوبوناچی را تعریف میکند.
در اینجا، $$ x [n]$$ سیگنالی است که مقدار آن زمان 0 برابر با ۱ و بعد از آن ۰ است. این دقیقاً همان سیگنال ضربه واحد است. معادله تفاضلی که گاهی رابطه بازگشتی نامیده میشود، اهمیت زیادی دارد، زیرا به ما این امکان را میدهد که به صورت ریاضی با سیستم سر و کار داشته باشیم.
نمودار بلوکی، یک روش گرافیکی برای نمایش سیستمها است. این نمودار از اجزای سیستم تشکیل شده است که با پیکانهایی به هم متصل میشوند و این پیکانها جهت گذر اطلاعات را نشان میدهند. سه جزء مهم در این نمودار وجود دارد:
- تأخیر: یک بلوک مستطیلی که یک تأخیر یا یک گام زمانی به سیگنال اعمال میکند.
- مقیاسبندی: یک بلوک مثلثی که سیگنال ورودیاش را با یک اسکالر تغییر مقیاس میدهد.
- جمعکننده: یک بلوک دایرهای که چند سیگنال را با هم جمع (یا از هم کم) میکند.
مجدداً دنباله فیبوناچی را در نظر بگیرید. میدانیم که به تعدادی حافظه برای آن نیاز داریم، بنابراین، استفاده از بلوک تأخیر برای آن ضروری است. همچنین، باید دو عدد را با هم جمع کنیم، به همین دلیل به یک جمعکننده نیز نیاز داریم. نمودار بلوکی دنباله فیبوناچی به صورت زیر است.
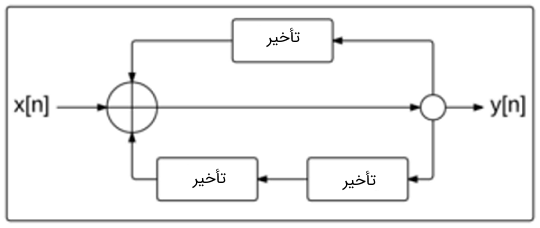
در این نمودار، دو حلقه فیدبک وجود دارد که یکی از آنها سیگنال را با یک گام زمانی تأخیر میدهد و دیگری با دو گام زمانی همین کار را انجام خواهد داد. جمعکننده نیز سیگنالها را با هم جمع میکند و خروجی را نتیجه میدهد.
معادله عملگر بسیار شبیه معادله تفاضلی است، اما از اجزای نمودار بلوکی استفاده میکند. معادله عملگر یک رابطه بین سیگنالهای ورودی و خروجی با استفاده از مقیاسبنی، جمعکنندهها و تأخیرهای نمودار بلوکی است. بنابراین، معادله عملگر برای سیستم دنباله فیبوناچی به صورت زیر خواهد بود:
$$ \large Y = X + \mathcal { R } X + \mathcal { R } ^ 2 X . $$
که در آن، $$ \mathcal {R}$$ برای نشان دادن تأخیر روی یک سیگنال ورودی مورد استفاده قرار میگیرد. این معادلات عملگری (که توابع سیستم نیز نامیده میشوند)، در پیشبینی رفتار سیستم مورد استفاده قرار میگیرند.
انواع سیستم ها
درست مانند سیگنالها، سیستمها نیز دستهبندیهای خاص خود را دارند که در ادامه آنها را بیان میکنیم.
سیستمهای خطی و غیرخطی
یک سیستم خطی است، اگر در شرط زیر صدق کند، که در آن، $$ x _ 1 (t)$$ و $$ x _ 2 (t)$$ به ترتیب، ورودیهای متناظر با خروجیهای $$ y_1 (t)$$ و $$ y _ 2 (t)$$ خروجی هستند:
$$ \large T \big [ a_ 1 x _ 1 ( t ) + a _ 2 x _ 2 ( t ) \big ] = a _ 1 T \big [ x _ 1 ( t ) \big ] + a _ 2 T \big [ x _ 2 ( t ) \big ] = a _ 1 y _ 1 ( t ) + a _ 2 y _ 2 ( t ) . $$
سیستمهای خطی معمولاٌ بسیار سادهتر از مشابه غیرخطی خود هستند. این سیستمها در نظریه کنترل خودکار، پردازش سیگنال و مخابرات مورد استفاده قرار میگیرند. به طور خاص، مخابرات بیسیم را میتوان با سیستمهای خطی مدل کرد.
سیستمهای متغیر با زمان و نامتغیر با زمان
سیستمی را متغیر با زمان میگوییم که رابطه ورودی و خروجی آن نسبت به زمان تغییر کند. معادلاتی که این دسته از سیستمها را مشخص میکنند، به صورت زیر هستند:
وقتی $$ y ( n , T ) = T [ x (n-t)] $$ برابر با تغییر ورودی و $$ y (n - t ) $$ تغییر خروجی باشد، آنگاه برای سیستمهای تغییر ناپذیر با زمان داریم:
$$ \large y ( n , t ) = y (n-t) $$
و برای سیستمهای متغیر با زمان، میتوان نوشت:
$$ \large y (n,t) \neq y ( n - t ) $$
سیستمهای تغییرپذیر با زمان برای بررسی جذاب هستند، زیرا خروجی آنها بیشتر به زمان بستگی دارد و خود سیستم نسبت به زمان تغییر میکند. تارهای صوتی انسان متغیر با زمان هستند. مدلسازی سیستمهای تغییرناپذیر با زمان بسیار سادهتر است.
سیستمهای خطی متغیر با زمان و نامتغیر با زمان
یک سیستم خطی تغییرناپذیر با زمان یا LTI سیستمی است که هم خطی و تغییرناپذیر با زمان است. این سیستمها در حوزه سیستمها بسیار مهم هستند. این به آن دلیل است که این سیستمها را میتوان به صورت ریاضی تحلیل کرد، به گونهای که برای هر سیگنال ورودی میتوان ویژگیهای خروجی را فهمید. همچنین، این سیستمها ترکیبی هستند و هر ترکیب از سیستمهای LTI خودش یک سیستم LTI است.
سیستمهای استاتیکی و دینامیکی
سیستمهای استاتیکی سیستمهایی بدون حافظه هستند. برای مثال، معادله یک سیستم استاتیکی به صورت زیر است:
$$ \large y [ t ] = 2 ^ { x [ t ]} . $$
این به آن دلیل است که خروجی $$y[0]$$ در لحظه کنونی فقط به ورودی $$x[t]$$ در لحظه کنونی بستگی دارد. از طرف دیگر، یک سیستم دینامیکی (یک سیستم با حافظه)، معادلهای مشابه زیر را دارد:
$$ \large y [ t ] = 2 \cdot x [ t - 1 ] . $$
در اینجا، خروجی $$y[t]$$ در لحظه کنونی دو برابر ورودی $$x[t-1]$$ در لحظه قبلی است، بنابراین، سیستم باید ورودیاش را به یاد بیاورد.
سیستمهای علّی و غیرعلّی
مشابه تفاوت بین سیستمهای دینامیکی و استاتیکی، یک سیستم علّی سیستمی است که فقط به ورودیهای گذشته و کنونی بستگی دارد. بنابراین، $$ y [ t ] = 2 \cdot x [ t - 1 ] $$ یک سیستم علّی است. یک سیستم غیرعلّی به ورودیهای آینده بستگی دارد؛ مثلاً $$y[t]=x[t+1]$$ یک سیستم غیرعلّی است.
سیستمهای پایدار و ناپایدار
یک سیستم پایدار سیستمی است که خروجیهای کرانداری به ازای ورودیهای کراندار داشته باشد. به عبارت دیگر، برای یک سیگنال کراندار، دامنه خروجی محدود باشد. بنابراین، برای مثال میتوان گفت که $$ y [n] = 2 \cdot x [n] $$ پایدار است.
یک سیستم ناپایدار است که به ازای یک ورودی کراندار، خروجی نامتناهی داشته باشد. این سیستمها را وقتی به درستی پیادهسازی کنیم، سبب یک سرریز پشته در برنامههای کامپیوتری میشود.
عملیات اساسی سیستمها
درست مانند سیگنالها، میتوان با سیستمها را ترکیب کرد و روی آنها عملیات انجام داد. توالی دو سیستم، دو سیستم را به صورت سادهای با هم ترکیب میکند. توالی دو سیستم $$ S _1$$ بعد از $$ S _ 0 $$ را در نظر بگیرید. در این سیستمها، $$Y$$ خروجی $$ S_ 0 $$ و $$ Z $$ خروجی $$S_1 $$ است. خروجی $$Y$$ سیستم $$S_0$$ به ورودی $$W$$ سیستم $$S_ 1 $$ وارد میشود. این عمل، در صورتی که هر دو سیستم در ابتدا در حالت سکون (برابر با 0) باشند، خاصیت جابهجایی دارند.
فرض کنید سیستمها اینگونه باشند:
$$ \large \begin {aligned} S _ 0 \mbox { : } Y & = \Phi _ 1 X \\ S _ 1 \mbox { : } Z & = \Phi _ 2 W , \end {aligned} $$
سیستم حاصل به صورت زیر خواهد بود:
$$ \large Z = \Phi _ 2 \cdot \Phi _ 1 X $$
جمع موازی یک راه دیگر برای ترکیب سیستمها است. فرض کنید سیستم $$ S_0 $$ دارای معادله $$ Y = \Phi _ 1 X $$ و سیستم $$S_1$$ دارای معادله $$ Z = \Phi _ 2 X $$ باشد. مهم است که سیگنال ورودی برای این عملیات مشابه باشند. بنابراین، جمع دو سیگنال خروجی به صورت زیر خواهد بود:
$$ \large W = ( \Phi _ 0 + \Phi _ 2 ) X $$
که در آن، $$W$$ خروجی جمع دو سیستم است.
به عنوان یک مثال، سه سیستم زیر را در نظر بگیرید:
$$ \large \begin {aligned} S _ 0 \mbox { : } A & = \Phi _ 1 X \\ S _ 1 \mbox { : } B & = \Phi _ 2 X \\ S _ 2 \mbox { : } C & = \Phi _ 3 W . \end {aligned} $$
دو سیستم $$ S_0$$ و $$ S_1$$ را با هم جمع کرده و حاصل آنها را با $$ S_2$$ متوالی میکنیم. خروجی سیستم نهایی به صورت زیر خواهد بود:
$$ \large Z = \Phi _ 3 ( \Phi _ 2 + \Phi _ 1 ) X . $$
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:










